Is Flourishing Predetermined?
Citations
21st January 2026
Abstract1
The Better Futures series argues that the chance humanity achieves a great future is low, but still achievable.3 That makes work on flourishing4 look especially valuable: there is plenty of room to make great futures more likely, but the default odds aren’t so vanishingly low that they’d be intractable to change. But our overall credence in flourishing might reflect some credence that flourishing is almost impossible, plus some credence that it’s very easy. If so, flourishing would be overdetermined, and hence less tractable2 to work on than we thought.
We consider how to formalise this argument, and ultimately conclude it’s a real but modest downwards update to the value of working on flourishing. Still, we hope the resulting model is a useful way to make sense of radical uncertainty about the difficulty of other problems.
Introduction
Imagine you're campaigning for a new bill to pass in your city council. Here are two scenarios:
- You've assessed that council members are genuinely undecided, and likely to vote based on their own judgment and constituent feedback. You place about even odds on the bill passing.
- You suspect the mayor has already formed a strong public position for or against the bill, and most council members will follow the mayor's lead. You don't know which way the mayor’s mind is made up, so you place about even odds on the policy passing.5
Although you place even odds on the bill passing in both scenarios, scenario (1) seems more ‘truly’ chancy. In (1), you might expect the outcome of the vote to be more sensitive to a wide range of small changes up to the vote. In (2), the outcome seems more predetermined one way or the other, so influencing just one or a few factors is less likely to influence the overall outcome.
Perhaps for that reason, efforts to lobby council members seem more effective in scenario (1) than (2). Whether you’re in a scenario more like (1) or (2) could matter for whether you choose to spend your money on this campaigning initiative.
With that in mind, here’s another thought experiment. Take millions of planetary civilisations similar to our own, and watch how they play out. Some fraction encounters a near-term catastrophe, the remaining fraction doesn’t. Of the remainder, some fraction flourishes, where we define “flourishing” as achieving a mostly-great6 future, conditional on survival.
Like before, you can form a probability distribution over the fraction of surviving civilisations that flourish. In the more intuitively ‘middling’ case, the true proportion of flourishing civilisations could take a range of intermediate values — perhaps because most civilisations could go either way, depending on fairly contingent factors. But in the ‘polarised’ case, most probability mass could be bunched up close to the extremes of zero and one — reflecting a guess that civilisational flourishing is either effectively doomed, or effectively guaranteed, but you’re unsure which.
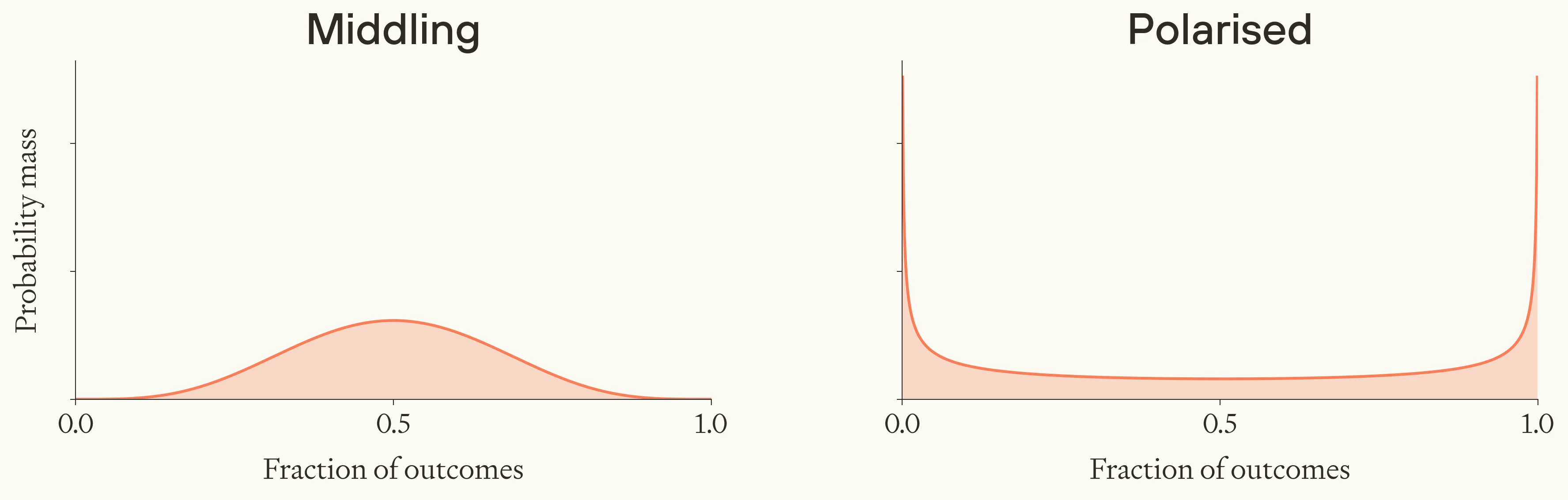
Comparing 'middling' and 'polarised' probability distributions.
Image
Now, the expected fraction of surviving civilisations that flourish (the mean of your subjective distribution) can be identical in both cases. But in the ‘polarised’ case, like scenario (2) above, flourishing intuitively seems more overdetermined one way or the other, and hence harder to influence.
Previous Forethought writing argued for the value of work to increase the chance of flourishing being comparable to the value of work to increase the chance of survival. But plausibly, we should have a very polarised probability distribution over a more ‘objective’ (or well-informed) likelihood of our own civilisation flourishing, conditional on survival. And that could imply that work on flourishing is much less tractable than you’d otherwise think. If the distribution is extremely polarised, that could make flourishing look significantly less promising to work on.
How likely is flourishing by default?
I’ll spell out the argument in some more detail. Here’s the structure:
First, consider all civilisations at roughly our stage of technological development.7 Among those that survive, what fraction eventually flourish?8 We can form a prior probability distribution over the true fraction, representing our subjective levels of certainty in different answers.
Next, we can ask what happens when we integrate specific knowledge about our own civilisation, by narrowing the reference class to civilisations indistinguishable to us from our own. Consider running very many copies of human civilisation today, with slightly varied starting conditions. We can ask: among the futures which survive, what fraction flourish?9 We can think of the question in terms of an evidential update to the first distribution based on observing we’re in our civilisation in particular.
Next, after narrowing the reference class, we can take the ‘objective’ fraction of worlds which flourish by default as a guide to the tractability of work on flourishing. That’s a contentious move, and I’ll discuss why it could be valid.
What fraction of human-level civilisations flourish?
Starting with the first question: among those civilisations at roughly our stage of technological development that survive, what fraction flourish by default? My own reaction is to feel wildly uncertain.10 I don’t have strong intuitions either way, and I’m similarly uncertain about important sub-questions:
- What, even roughly speaking, does this reference class of civilisations look like?
- Will flourishing turn out to be surprisingly achievable in technological terms?
- Are there self-reinforcing dynamics which point towards flourishing?
- Are there self-reinforcing dynamics which point away from flourishing?
And so on.
Choosing an uninformative prior
When forming a prior over an objective probability that we’re very uncertain about, it makes sense to choose an uninformative prior.
Intuitively, an uninformative prior should spread our credence over order of magnitude in odds more evenly than a uniform prior over probability. After all, the sense of radical uncertainty here tracks the sense that roughly 10,000:1 odds aren’t much more or less plausible-seeming than even odds, or roughly 1:10,000 odds. But a uniform distribution in probability implies that an “objective” probability lower than 10,000:1 odds is about a thousand times less subjectively plausible than a probability between 45–55%, which seems overly confident.
Many candidates for an uninformative prior fit that intuition. One especially natural choice11 is the Jeffreys prior, which in the binomial case is the beta distribution with . Let’s take that as our starting point.
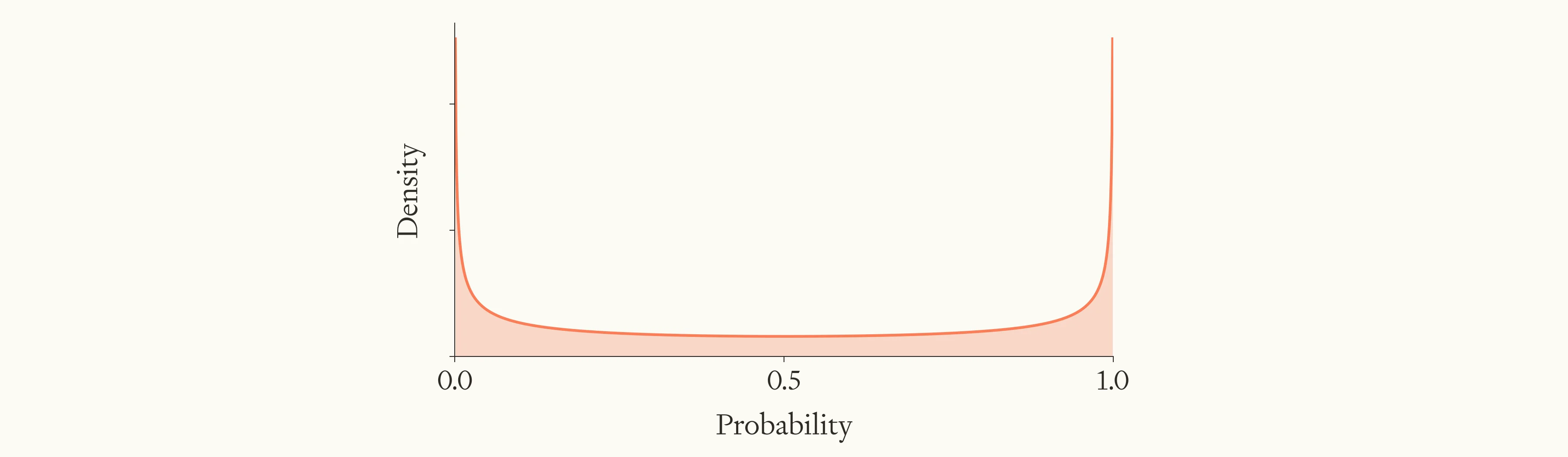
The Jeffreys prior.
Image
Models of flourishing
Now we can get a notch more concrete by considering possible models of flourishing in particular, and seeing what kinds of distribution they generate.
The multiplicative model
One model, suggested in previous writing, is that the value of the future could be well-described as a product of many independent factors. This would suggest the value of a given civilisation has a heavy-tailed distribution, with very few worlds passing the mostly-great bar.12
Now, suppose instead that we’re uniformly uncertain about the threshold in value required to count as mostly-great, and we imagine that civilisations are distributed in value in some heavy-tailed way, such as you’d get if value were the product of many independent factors. Then the resulting distribution over the fraction of civilisations which exceed the threshold will also be heavy-tailed.
That said, a truly heavy-tailed distribution in value, plus uniform uncertainty about the value threshold, wouldn’t give a U-shaped distribution in the fraction of mostly-great futures: this distribution is especially confident that the fraction is low, and vanishingly confident that it approaches 1.13
Alternatively, we might be uncertain about the degree of correlation between the factors which multiply to give a measure of value, for each civilisation. If the factors are correlated enough, then most civilisations flourish. That would add much more mass to the flourishing fraction being middling or high. But the result still wouldn’t be U-shaped — that would require, for example, placing some credence on the threshold being passed however the factors shake out.14
The basin model
On the other hand, we might imagine there are self-reinforcing dynamics which point upwards towards mostly-great futures, such that once a given civilisation passes some threshold, it has a substantial chance of achieving a mostly-great future.
On the simplest model, we might imagine that civilisations initially enter a ‘basin of attraction’ towards flourishing with some likelihood, where flourishing is guaranteed if they enter the basin of attraction, and impossible otherwise. If we were very confident about the likelihood of a random civilisation entering the basin of attraction, our subjective prior distribution over the fraction of flourishing civilisations would then cluster around that likelihood.
Sufficiently good epistemic practices could be one example of a self-reinforcing, bootstrapping dynamic. Starting with some reasonably effective methods for refining beliefs and theories, better beliefs and theories might help spot flawed methods and assumptions, and so on, like the cumulative and error-correcting methods of the empirical sciences. Other starting combinations of beliefs and values might have “self-sealing” dynamics. Similarly, starting with functional-enough institutions for cooperation could promote trust just enough to improve those institutions in turn, in an upwards spiral.16
However, if there is such a basin of attraction (or if there are many), we’re ignorant about the likelihood of entering it. So it could be be more appropriate to spread our credences evenly across the order-of-magnitude size ratio between the region of the space of surviving civilisations representing a basin of attraction, with the rest of the space, between two reasonable-seeming bounds. This is a uniform distribution in log-odds between bounds.15
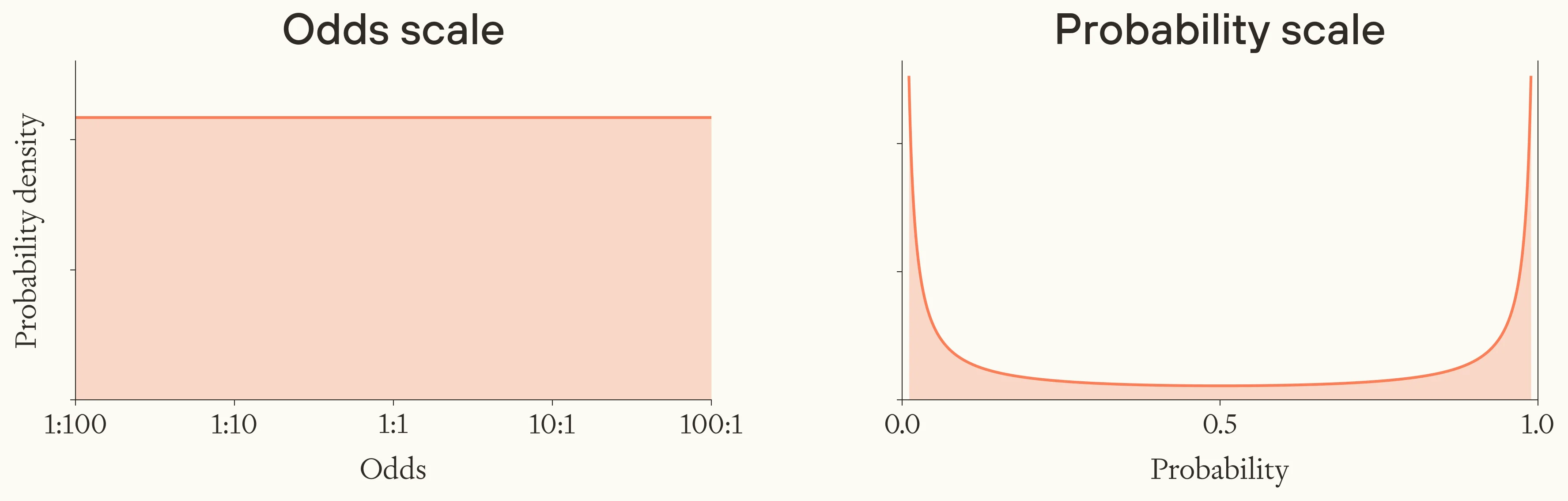
A uniform distribution in log-odds between a lower and an upper bound. Shown in log-odds space (left) and probability space (right).
Image
Finally, there’s no special reason to think our subjective distribution should be symmetrical. On the one hand, remember that we’re conditioning on civilisations which survive, which I expect should mean shifting more weight onto higher fractions, mainly because survival suggests more civilisational competence, and I’d expect civilisational competence to also make flourishing more likely. In other words, I expect flourishing and survival to be correlated. On the other hand, there are some reasons to think that flourishing is simply very difficult, in the sense that our expected fraction of surviving civilisations which flourish (the mean of the distribution) is very low. The second factor weighs much more strongly for me.
All things considered, then, my best guess at a reasonable distribution places most weight very close to zero, with reasonable credence spread across middling and high fractions, and perhaps a small bump around higher probabilities.17
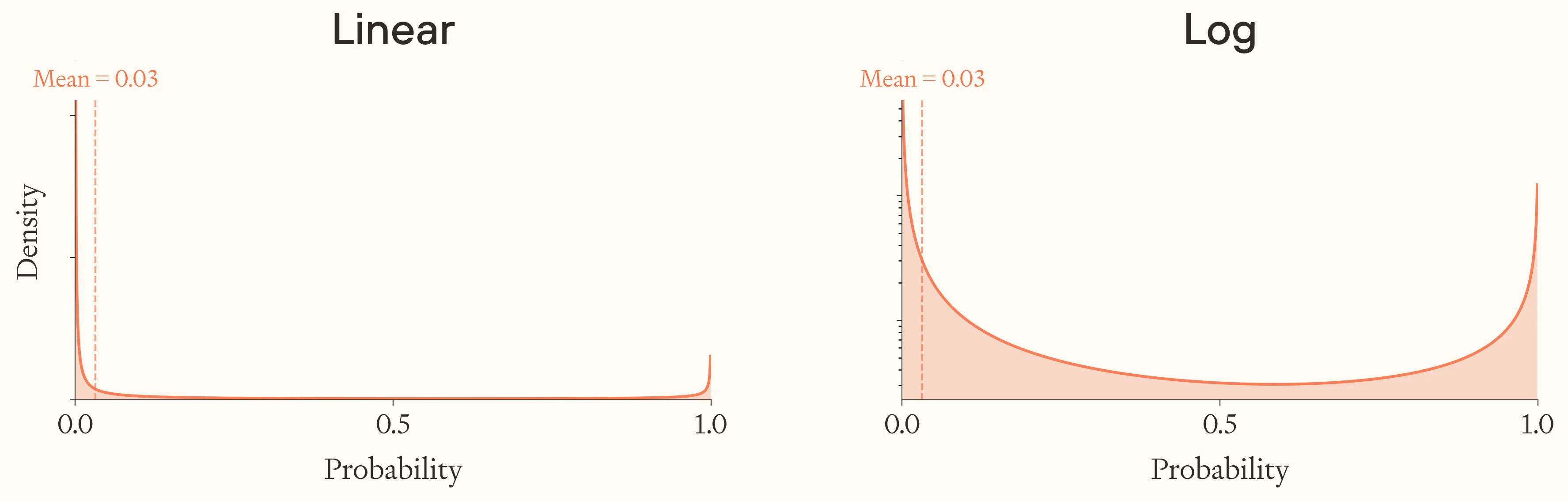
A subjective distribution over the fraction of human-level civilisations which flourish (linear and log scale).
Image
The models which generate big spikes at both ends of the distribution are qualitatively plausible, but I found the parameter values which generate clearly U-shaped distributions are somewhat contrived in practice. In practice, my best-guess parameter values put far less probability mass in than , and the ‘middling mass’ outweighs .18
Will our own civilisation flourish?
Let’s turn to the second question: consider running many copies of human civilisation today, and varying the starting conditions in a bunch of virtually unnoticeable ways. Among those futures which survive, what fraction flourish?
In a sense, this is the same question as above, but the domain of civilisations has been narrowed all the way to just those civilisations indistinguishable from our own. It’s as if you began by knowing you are in some randomly chosen civilisation, and now you learn the civilisation you’re in looks like this, and you’re wondering how to update your distribution.
Firstly, you have lost differences between civilisations as a major source of variance between outcomes. You could think that the fate of any indistinguishable set of civilisations is largely fixed by the time they reach human-level technology, but there is a close-to-even mix of civilisations guaranteed to flourish and doomed not to. Then, on narrowing the set of civilisations to be indistinguishable, you know the fraction of these civilisations which flourish will be much closer to the extremes. To the extent you learn anything about which kind of civilisation you’re in, your distribution becomes more polarised.
But the new distribution doesn’t have to be more extreme: the fraction of civilisations like ours which flourish could more plausibly be a more middling number than the fraction of all human-level civilisations.19
And indeed, human civilisation seems more chancy and middling than it could have been, whether that makes us unlucky or lucky compared to other civilisations. In other words, it really looks like flourishing20 hangs in the balance, in a way which could easily not be true.
I’ll spell that out. On the one hand, our world isn’t on any obvious course for narrowly prescriptive global government, or total breakdown of good will and cooperative intent, or draconian measures limiting scope for exploration and ambition. On the other hand, ours is not a civilisation that “has its act together” in any conspicuous sense; whereas we could have found ourselves in a reflective, cautious, cooperative, and open-minded civilisation. Since we can imagine finding ourselves in a more predetermined situation, that suggests the share of civilisations just like ours which flourish is more middling than the share of all civilisations which flourish.21
So, we have two considerations to balance: one suggests the updated distribution should be more polarised, and the other suggests it should be more middling. My best guess is that it should be somewhat more middling.22 Here’s a sketch,23 where the original (all civilisations) distribution is also shown in grey.
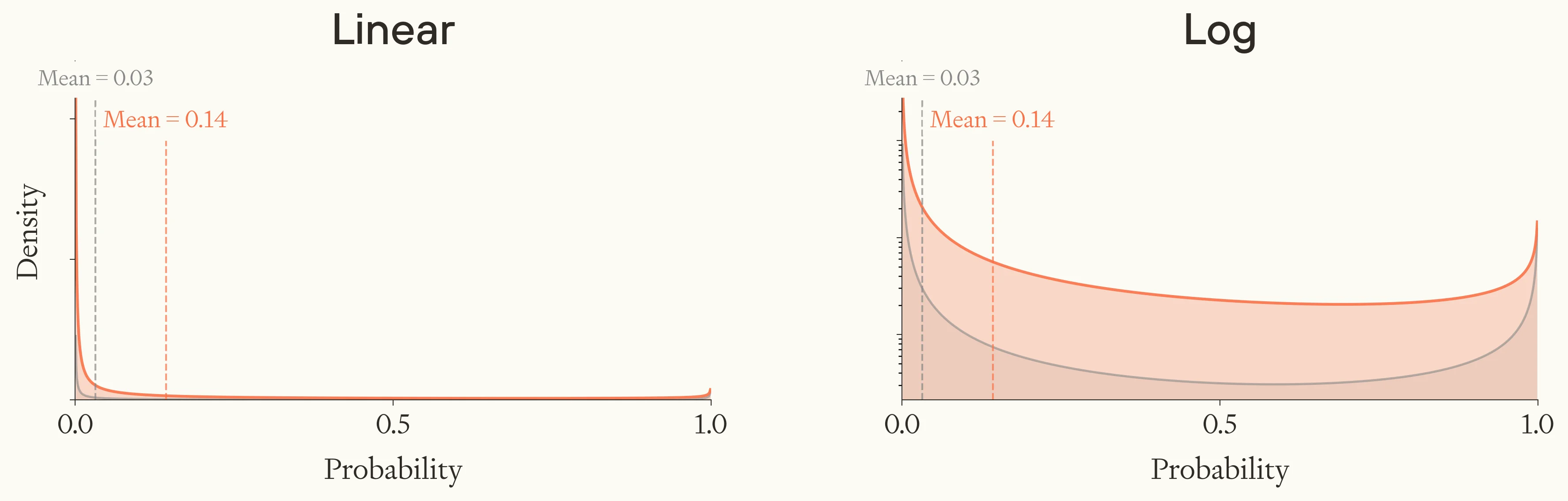
A subjective distribution over the fraction of near-identical civilisations to ours which flourish (orange), compared with the same distribution for all human-level civilisations (grey). Both linear and log are shown.
Image
The ‘objective’ chance of our own civilisation flourishing — understood as the true fraction of surviving futures like ours which flourish — still looks most likely to be close to zero, with perhaps 10% credence on a ‘middling’ probability within , and a small second mode approaching .
From probability to tractability
Remember that the motivating intuition for this line of thinking is that, if the ‘objective’ likelihood of flourishing is very low or very high, then we should also expect pro-flourishing efforts to be less tractable than if the objective chance24 were some middling fraction. So a polarised distribution suggests lower tractability than a middling one. In the intro, I gave the example of an upcoming election, which fits the intuition.
Next, I’ll describe a model which we can apply to flourishing.
The hidden-difficulty model
First, we assume the objective chance of some desired outcome is the logistic function of the sum of a 'baseline' parameter, plus a ‘control’ parameter representing the shift we make through deliberate effort. In other words: with a unit of effort, you move the log-odds of the outcome by the same amount, whatever the starting probability.
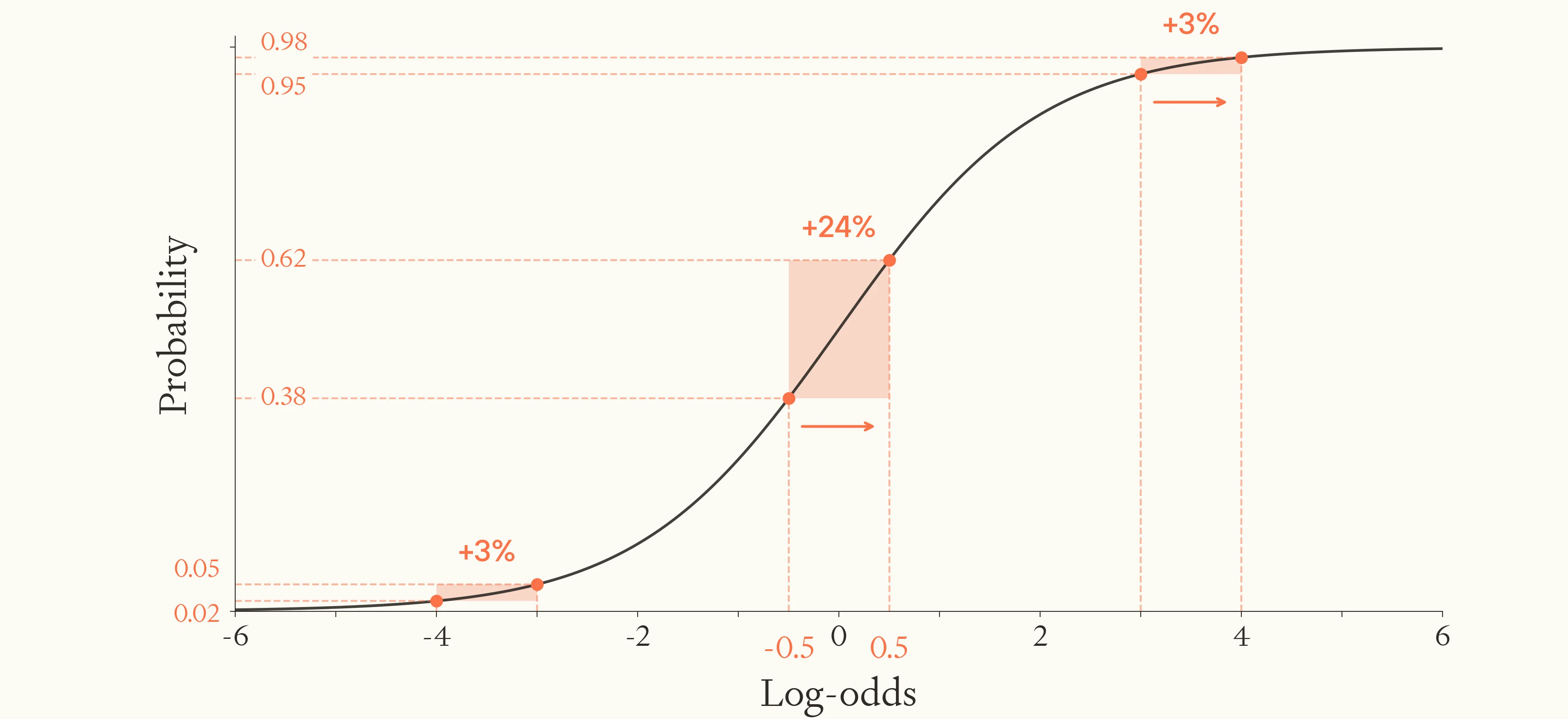
Converting between log-odds and probability. The same shift in log-odds results in a larger shift in probability when the initial probability is more middling.
Image
Here, the baseline parameter represents the default log-odds of the outcome, and the ‘control’ parameter represents how moveable the log-odds are with a unit of effort.
The marginal gain in probability from a unit of effort, from now on movability,25 is then: .26 Hence, the same unit of effort moves the needle least when is close to 0 and 1, and the most when .
Furthermore, we're uncertain about the objective chance of the desired outcome, so we’re also uncertain about the movability of the objective chance with a unit of effort.
We can however consider the expected movability, given your subjective distribution over the objective chance of the outcome. Where is the expected value of , and factoring for the control parameter , it turns out that the expected movability is equal to minus the variance of your distribution.27
It follows that, fixing , adding uncertainty about the true likelihood always decreases the expected movability of making the desired outcome more likely. The expected movability can get arbitrarily close to zero as the distribution gets more polarised, but it’s never higher than when you’re certain of .
Limitations of the hidden-difficulty model
In this model, even a very low subjective probability doesn't imply low movability,28 because your level of influence over log-odds () can be high.29 Similarly, a middling subjective probability doesn't imply high movability, because your level of influence over log-odds could be low,30 or your distribution over the objective probability could be very polarised. So to shed any insight on the expected movability of a problem, you need a way of estimating or controlling for the control parameter ().
If we try to describe various real problems in terms of this model, we'll notice that the control parameter () varies enormously between problems. Moreover, it can also vary within a problem — additional units of effort might shift the log odds by very different amounts.31
So the hidden-difficulty model is most useful when there is some notion of an ‘objective’ probability of the desired outcome, and when a unit of effort will move the log-odds by roughly the same amount whatever the objective probability, and when this unit of effort can be pinned down.32 Then the model can tell us useful things about how the expected movability of making the outcome more likely depends on the shape of our uncertainty over its actual default likelihood.
Otherwise, I’m definitely not saying that this model is widely applicable, in the way that (for example) the ‘ITN’ framework is designed to be.
However, the model does seem decently well-suited to flourishing. In fact, even if we’re also very uncertain about the level of control we’re likely to have over flourishing in log odds, we can do two things: we can figure out the downward update to movability after switching from a naively certain to uncertain distribution over the objective probability of flourishing; and we can compare flourishing with survival by assuming the level of control to be similar. I work through both cases next.
Applying the model to flourishing
Imagine we began by naively thinking we can be confident of the objective chance of flourishing by default. Then, we integrate the point above: that we should expect the true movability to be lower than we thought.
The downward penalty after updating to represent our (very wide) uncertainty about the objective chance of flourishing is just the variance of the new distribution, as a proportion of .33
Using my best guess distribution of the objective chance of flourishing, I find that updating to a widely uncertain distribution over the objective probability reduces the expected movability by about 60%.34
Comparing flourishing with survival
In the previous section, I suggested a model for the intuition that radical uncertainty about the default likelihood of a desired outcome reduces its expected movability, given some assumptions. Since we’re radically uncertain about the likelihood of flourishing, we should be correspondingly more pessimistic about the movability of that default likelihood.
In the framework I’m using, flourishing is contrasted with survival. Recall that survival means not entering a state much closer in expected value to extinction than to a mostly great future, and which seems to most people today like a disaster which destroys almost all potential value. Flourishing means reaching a mostly-great future, conditional on survival.
The same argument above also applies to survival. Parallel with flourishing, we can imagine slightly varying our present civilisation in many indistinguishable ways, and then ask what fraction of those civilisations would ultimately survive, whether or not they go on to flourish.
Just like before, our distribution over the true fraction is going to be spread out. It’s not crazy to imagine that survival is really close to guaranteed: the risks we know about are terrible but recoverable, and the potentially irrecoverable risks like overt forms of AI takeover turn out to be easy to avert, or not likely in the first place, like the millennium bug. On the other hand, it’s hard to entirely rule out the most pessimistic stories about the coming century — for example, that if anyone builds superintelligent AI, we’re doomed. A 50% subjective credence in survival doesn’t imply certainty that if we keep re-running the tape, we survive 50% of the time. Things could be (and likely are) more pre-ordained either way.
So, the same downward update to expected movability applies; but it could be a much larger or smaller update compared to the flourishing example. In fact, I guess it’s a smaller update. The reason is that we know more about the chance of survival, whereas the chance of flourishing depends more on theoretical, philosophical, and downright unknown considerations which we should be widely uncertain about.35
By contrast, we arguably have more observational evidence about the chance of survival. We’ve plausibly seen situations — like nuclear near-miss incidents — where humanity already came quite close to global catastrophe. That seems like evidence that solidly rules out worlds where survival is totally guaranteed.36 On the other hand, it’s not very difficult to tell a story where humanity survives. Because we know we can survive at current technology levels, one story would be that technological progress broadly stalls out at current levels, only cautiously progressing along the specific directions needed to keep flourishing alive as a possibility.
For the sake of concreteness, here’s a reasonable-seeming subjective distribution for survival:37
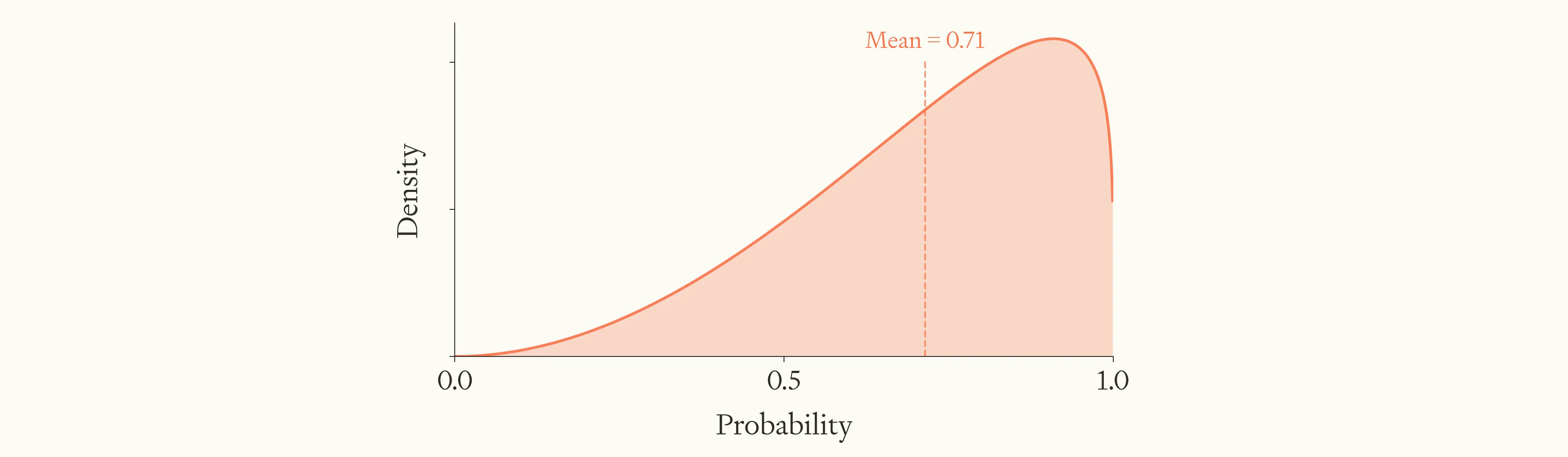
A subjective probability distribution over the fraction of near-identical civilisations which survive.
Image
This distribution has a lower variance to my distribution for flourishing, and a less extreme mean. So if we imagine that the naive expected movabilities of flourishing and survival are initially equal, then we should conclude that the penalty to the expected movability of flourishing is bigger than the penalty to survival.38 In other words, after making this update, working on survival looks about twice as promising in relation to movability than it did before.
Prioritising between survival and flourishing
The value of making flourishing more likely depends on the chance of survival, and vice-versa. To simplify things, we can approximate the value of the future just as the chance of surviving and then flourishing: the product of the two likelihoods.39
The marginal value of increasing the chance of flourishing with a unit of effort, then, is just the movability of flourishing multiplied by the chance of survival; and vice-versa for the marginal value of making survival more likely.
If we assume survival and flourishing are equally tractable, then it follows that the less likely factor is more relatively valuable to work on, and increasing the chance of one factor is more absolutely valuable in worlds where the default chance of the other factor is higher.
Instead we can assume an equal level of control over log-odds,40 but not movability. Then, expected movability is lower when the expected likelihood of the outcome being considered is more extreme.41
We can combine these points to understand how, all else equal, the value of working on flourishing and survival depends on their default likelihoods.42
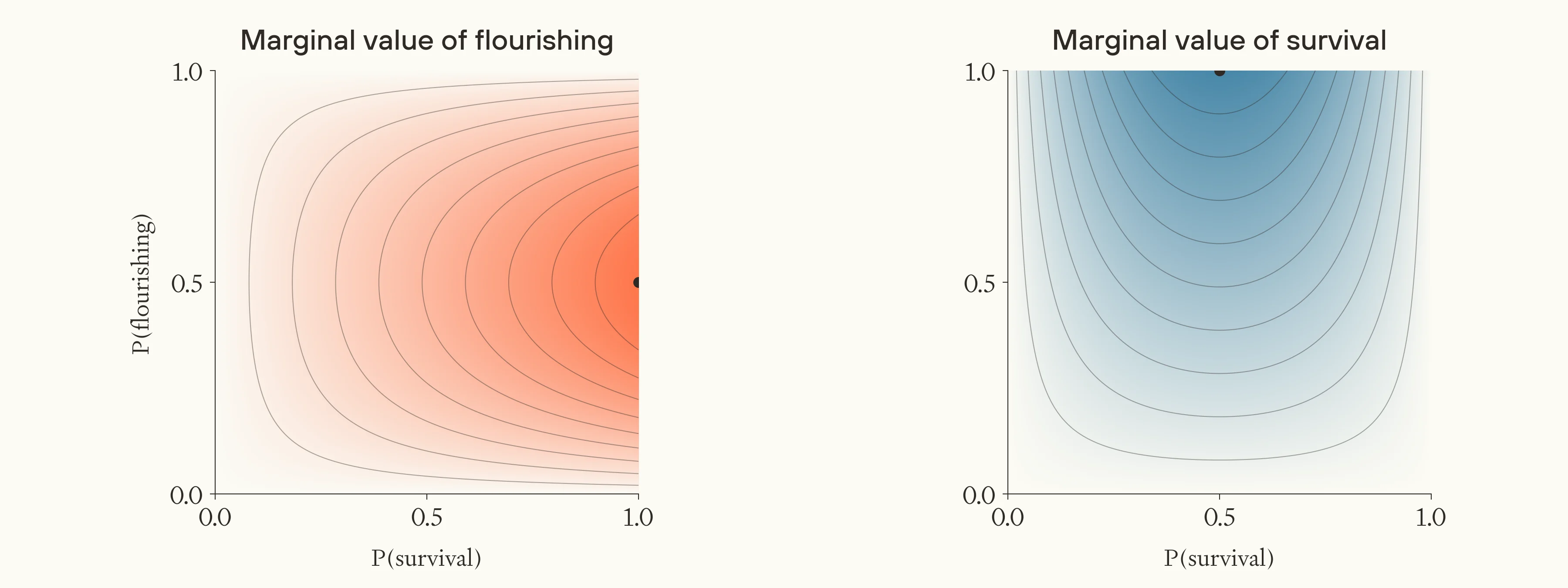
The marginal value of applying the same unit of effort to increasing the chance of flourishing and survival, given different background probabilities.
Image
We can also look at the absolute difference in value between working on flourishing and survival, in terms of the value of a mostly-great future. The graph below shows this.
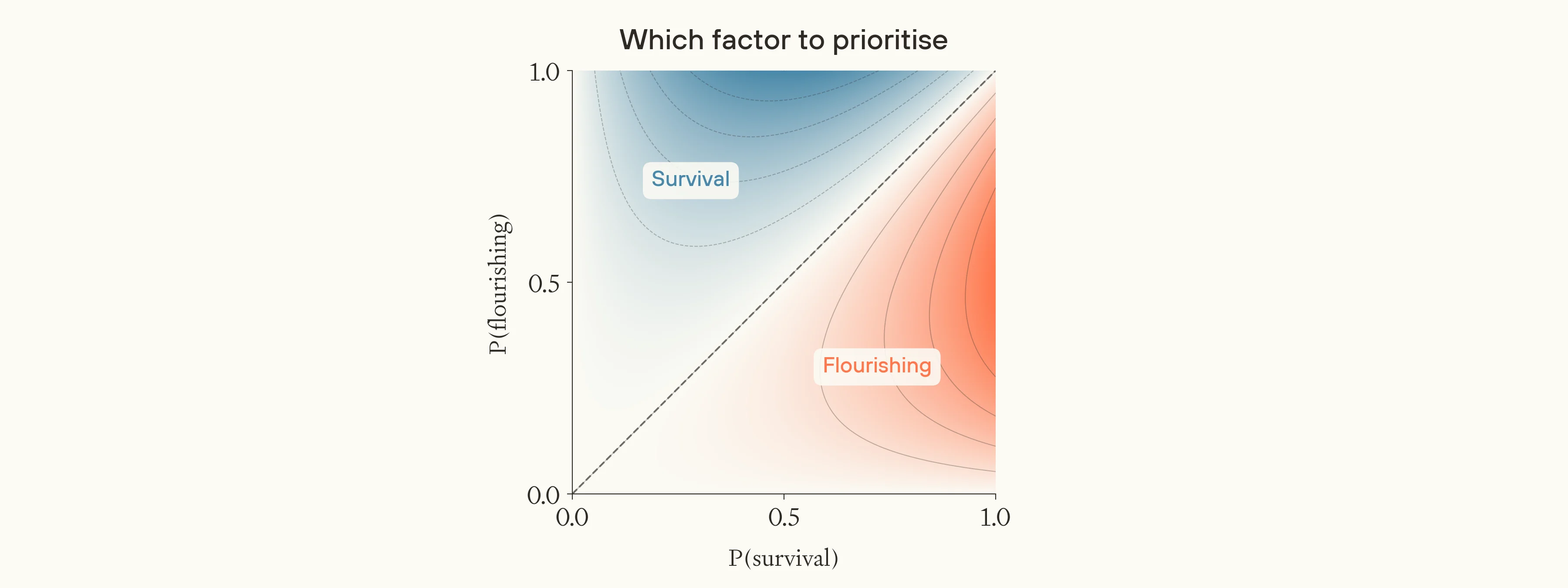
The absolute difference in the marginal value of applying the same unit of effort to increasing the chance of flourishing versus survival, given different background probabilities.
Image
Movability is higher towards middling probabilities, and the stakes are higher when the other factor is more likely. Thus, working on flourishing looks more absolutely valuable when the chance of flourishing is middling, and the chance of survival is high. Working on survival looks more absolutely valuable when the chance of survival is middling, and the chance of flourishing is high. When both factors are low, the stakes of the future seem overall lower, and vice-versa. Moreover, the relative importance of working on flourishing is always higher when the chance of survival is higher, and vice-versa.43
Interactions between survival and flourishing
The effects of different interventions on one factor might in practice depend differently on the default likelihood of the other factor. For example, perhaps some way to make flourishing more likely has a bigger effect on the chance of flourishing in worlds where the chance of survival is low. In such cases, the best interventions might not always be the interventions with the highest expected movability.
Here’s an example: suppose you’re choosing between interventions to increase the likelihood of survival, where some “pessimistic” interventions improve the chance of survival the most in worlds where the chance of flourishing is low, and other “optimistic” interventions work best when the chance of flourishing is high. Even if the optimistic interventions have less expected effect on the chance of survival, they might nonetheless be more valuable in expectation, because they pay off in worlds where it’s more valuable for them to pay off.
The rule of thumb is to act like you’re optimistic about the default chance of the other factor panning out. And that’s a more generally applicable heuristic, since the reasons don’t especially depend on the hidden-difficulty model.
Conclusion
Often, it’s hugely uncertain how likely a problem is to be solved by default: the ‘true’ likelihood may be very likely close to either impossibility or inevitability. In those cases, working on the problem looks less valuable than it would otherwise.
At first glance, this line of thought presents a reason to be more pessimistic than before about the value of working on flourishing, as compared with other potential global priorities. I suggested one reasonable model of the intuition, and on my own numbers, I found that it should indeed make us less than half as optimistic about the value of flourishing before integrating this lesson.
Since the update to survival seems much smaller, I find that survival comes out looking about twice as good relative to flourishing, compared to how they looked before. Interactions between the two factors could matter, too: when intervening on one factor, we should often plan “optimistically” with respect to the other.
Reflecting on this whole framework, and the model of tractability, I feel pretty cautious about drawing any big conclusions. ‘Flourishing’ and ‘survival’ themselves are extremely abstract categories, and it’s possible that these abstractions wouldn’t hold up well if we really understood the situation. Contemplating the value of abstract categories (like “existential risk reduction”) can be a useful orienting device. I think we should learn from the most robust and relevant abstract considerations, but then pay most attention to the case-by-case promisingness of concrete interventions. The rest, when we’re so uncertain, is noise.
Frankly, I'm also struck by how small the penalties to expected movability seem to be on this model, even for probability distributions which appear almost totally predetermined on their face. When we’re so wildly uncertain, even a 2x update in either direction feels like small change.
Still, I think something like the hidden-difficulty model is often relevant when prioritising between problems, and deserves to be part of the toolkit for problem prioritisation.
I’ll highlight two rules of thumb which I think apply, at least in an “all else equal” sense, more widely. First, when you’re trying to bring about an outcome of very uncertain default likelihood, consider that the outcome is basically overdetermined already. Thus, prioritise problems whose difficulty you know, or on bringing about outcomes whose default chance you know. Second, when acting on one of several factors that multiply, act optimistically about the other factors.
Acknowledgements
Owen Cotton-Barratt wrote the original note explaining the central ideas. Carlo Leonardo Attubato suggested the formal model, and is thus credited as a co-author. Fin wrote the text.
Major credit also goes to the roughly 40 people who elaborated on Owen’s ideas as part of a work trial for Forethought. If you are one of those people and would like to be credited by name, please let me (Fin) know.
Thanks also to Max Dalton, Rose Hadshar, Mia Taylor, and Stefan Torges for comments. Errors are mine.
Appendix — the hidden-difficulty model
This section walks through the “hidden-difficulty” model in more detail. The model is originally due to Carlo Leonardo Attubato.44
Recall that the objective chance of some outcome is represented as the logistic function of the sum of a 'baseline' parameter , plus a parameter representing the shift made through deliberate effort on top of the expected level of effort:
The marginal gain in probability from a unit of effort, is then:
Movability
We use “movability” to refer to the quantity . We take an uncertain subjective distribution over the value of , assuming is independent of . Then:
Note:
Thus, the expected movability is equal to minus , all multiplied by the control parameter .
Given this, we can place bounds on expected movability:
Demonstrating the lower bound:
Since , we have for all , so .
By definition, .
Since and by stipulation, it follows that .
The upper bound is easier to see, since is never negative.
The expected movability approaches zero when , which you get when you're sure is either 0 or 1; that is, is perfectly predetermined either way (a Bernoulli random variable).
On the other hand, expected movability approaches its maximum firstly when (you’re certain of the objective probability), and secondly when ( is maximised at by symmetry).
One upshot of the model is that when your expected value of is very close to 0 or 1, then the movability of changing it must be low (holding fixed). On the other hand, when your expected value of is middling, the expected movability could be low or high, and it's more important to consider the shape of your distribution over (and its variance in particular).
Assumptions
The formula above for expected movability assumes that the control parameter is independent of the objective probability . To see why, suppose depends on , written as . Then:
Unlike the independent case, we cannot factor out of the expectation. Instead:
Where is the probability density over . This integral does not generally simplify to .
Comparing survival and flourishing
Here’s a table to compare the value of survival and flourishing, assuming an equal control parameter .
| Low default flourishing | Medium default flourishing | High default flourishing | |
|---|---|---|---|
| Low default survival | Both unimportant, both less movable. | Flourishing more movable, survival more important. | Both less movable, survival more important. |
| Medium default survival | Survival more movable, flourishing more important. | Both important, both movable. | Survival more movable, survival more important. |
| High default survival | Both less movable, flourishing more important. | Flourishing more movable, flourishing more important. | Both especially important, both less movable. |
Movability vs tractability
Movability, as I've defined it, roughly tracks the common-sense notion of tractability.
But "tractability" happens to have a formal definition as part of the importance (or scale), tractability, and neglectedness (or ITN) framework. This definition is related but distinct from movability — and that's why I used a new term for movability.
On the ITN framework, tractability is defined as the elasticity of progress on a problem with respect to effort on the problem:
is the percentage of the entire remaining problem being solved (by a unit of effort), which in our case is . is that unit of effort as a percentage of total effort, .
In this context, the "problem" being solved is the remaining objective chance that we don't reach the desired outcome (survival or flourishing in our case, the outcome with probability ). So when we increase on the margin by , the percentage of the remaining problem being solved is . The percentage increase in total effort is . Thus:
Recall:
Note:
Thus:
And, equivalently:
Two observations here. First, tractability scales with total effort, whereas movability is defined in terms of absolute marginal effort. This makes sense: when total effort so far is high, yet the objective probability still moves a lot in response to more effort, it must be very tractable. Whereas if your marginal unit of effort follows very little effort so far, the problem may be movable only because it's extremely neglected (in ITN terms). By contrast, movability bakes in neglectedness: a problem of fixed tractability is more movable if it's more neglected.
Second, tractability factors out the absolute magnitude of the difference in probability, only considering what fraction of the remaining gap gets closed. Whether a unit of effort shifts 98% to 99% or 80% to 90%, those problems are equally tractable, but differ in movability by a factor of 10.
In other words, when comparing interventions aimed at making the same outcome more likely, then movability is proportional to ITN. When comparing interventions and outcomes, the product of movability and the full counterfactual value of the outcome is proportional to ITN — since and :




