Space Debris and Launch Denial
Citations
17th December 2025
This is a rough research note – we’re sharing it for feedback and to spark discussion. We’re less confident in its methods and conclusions.
Introduction
Nearly 15,000 tons of human-made objects are orbiting Earth at this moment. Some are functional satellites, others are fragments of debris. Runaway “Kessler syndrome”, or simply space debris accumulating much more even without runaway effects, could render satellite operations in preferential, high-demand orbital regions prohibitively expensive or practically impossible. In more extreme cases, we might also wonder whether it becomes practically impossible to leave Earth for outer space, because of the need to transit through these orbits. Given the prospect of much accelerated activity in space after a potential industrial explosion, both possibilities could have big implications.
I’ll consider two main scenarios. First, a scenario where activity in space by many actors leads to buildup of orbital debris, though no major actors intended for it. Second, a scenario where some actor deliberately generates or positions orbital debris: for its sheer destructive potential, or perhaps as a means to raise the cost of launching through orbit to outer space. I'm limiting my implicit timeframe to roughly the next two decades.
In both cases, humanity's potential could be diminished. In the accidental case, we could lose access to important uses of low-Earth orbit, like remote sensing capabilities used for verifying arms control agreements. In the deliberate case, a bad actor could use the threat of generating massive amounts of debris as a source of illegitimate leverage. If they could make launches through Earth prohibitively difficult for the rest of the world, they could perhaps then enforce their first-mover advantage in settling space; effectively and perhaps indefinitely plundering access to outer space. That's not to mention the more obvious and prosaic cost of losing access to the communications, imaging, and security benefits that access to orbit affords those on Earth.
After looking into these questions, here are some bottom-line conclusions:
- Natural (non-deliberate) Kessler syndrome looks plausible with much increased launches into space and without more robust mitigations. I think it's more likely than not that it would occur within, say, 10 years of an industrial explosion without much improved avoidance or cleanup technologies, and with persistent non-compliance with traffic and disposal rules (and less likely than not otherwise).1
- However, I expect the aftermath of even fairly severe kinds of accidental Kessler syndrome would not make launch through orbit into outer space practically impossible; in fact I expect they would make launches negligibly more costly (ignoring the value of the payload).
- Largely because of this, I see low risk to Earth-departure capability from attempts to induce Kessler cascades without adding vastly more debris mass into orbit, such as via targeting ASATs at massive objects in orbit. Such actions could raise launch costs and constrain schedules, and may temporarily close specific ascent corridors, but they are unlikely to block departure altogether. By far the biggest cost of such strategies, in my view, is destroying satellites (and making them far more expensive to operate).
- I am somewhat more concerned about cases where some actor directly launches very large quantities of fine-grained debris into orbit, in order to either cause general damage to satellites, or specifically to try to make launches beyond Earth more costly for the rest of the world. If such an actor could establish the first self-sustaining presence beyond Earth beforehand, that could maybe afford them a first-mover advantage where otherwise they wouldn't have one.
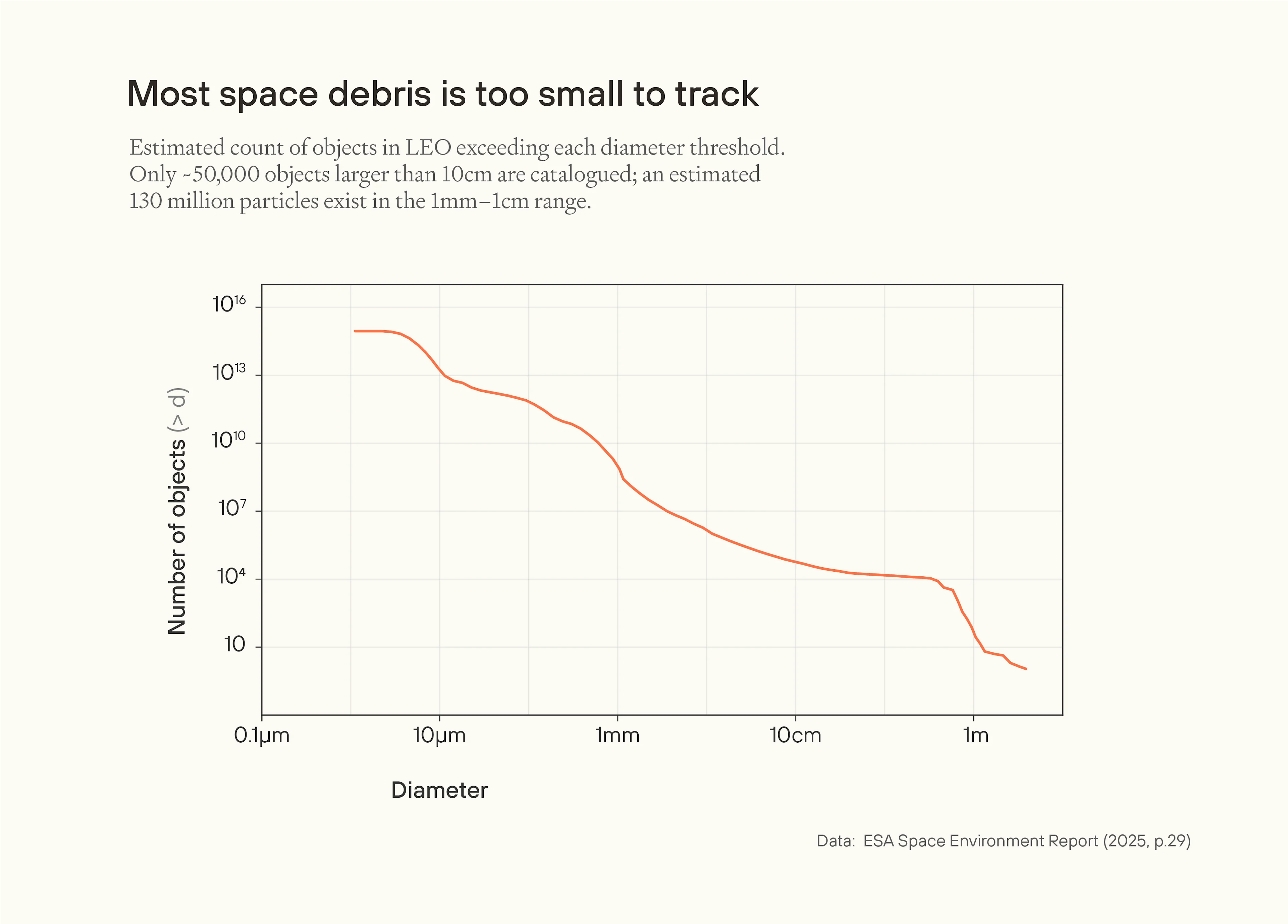
- As debris increases, there are practical thresholds in terms of fragment flux (especially 1 mm–1 cm "lethal non-trackable" particles), along ascent paths where launch risk and cost rise sharply unless protection improves. These thresholds are not just a function of total mass in orbit, but by the size-and-altitude distribution of debris, and the effectiveness of avoidance and shielding. Without improvements to avoidance and shielding for launch vehicles, I expect around a million tons of natural debris in a worst-case size and altitude distribution would be enough to render conventional Earth-to-space launches unfeasible.
- When considering launches through orbit, I think shielding is a major mitigating factor, and could in the end make it very difficult to prevent launches with even large amounts of deliberately released space debris. Avoidance (through tracking flight paths) could also help, but only up to intermediate levels of debris flux.
- That leaves deliberately spreading debris (or otherwise triggering Kessler syndrome) as a way for a rogue state to threaten the rest of the world through sheer damage to objects in LEO. This is concerning, and worth taking steps to deliberately mitigate. However, I'm unsure why it would be more attractive than other ways to cause major and diffuse global damage.
- Overall, provisions to prevent debris-creating actions seem well-justified, likely fairly easy to implement, and don't have obvious downsides. One saving grace is that deliberately injecting thousands of tons of debris into orbit is difficult to do quickly or in secret (unlike releasing a dangerous pathogen, for example), so monitoring and verification agreements look relatively feasible.
Some basic context on space debris
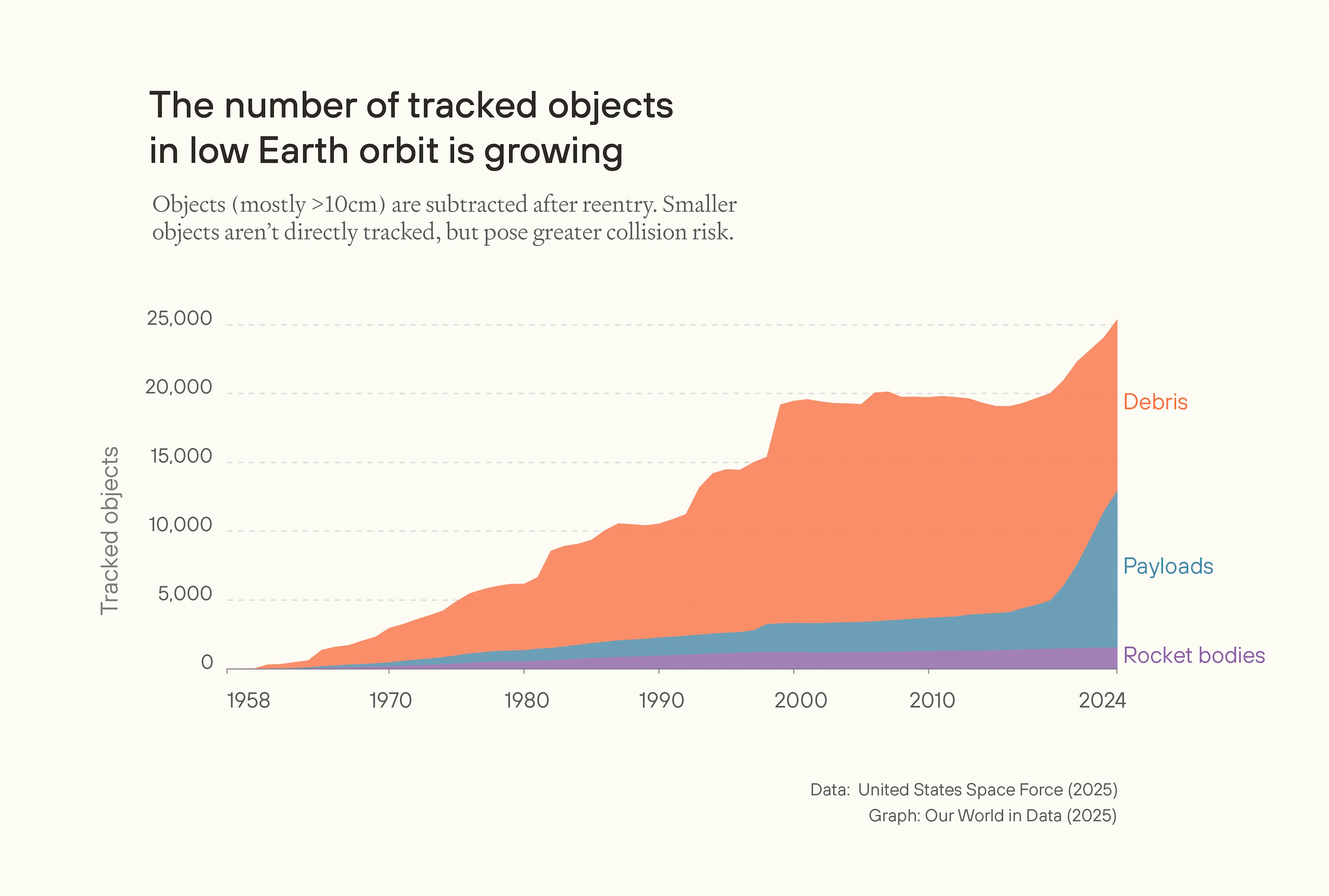
Virtually all orbital space debris — solid matter in orbit around Earth — is put there by humans; overwhelmingly (to date) from satellites. Of all satellites launched into orbit (well above 20,000), more than 11,000 remain active, and about 3,000 are defunct and un-steerable, but remain in orbit; the remainder having been destroyed or returned to Earth.
Because colliding with even a tiny piece of matter can be mission-ending, splitting one object into many small fragments poses a much larger risk of further collisions. Sometimes small explosions (like fuel tank ruptures) fracture larger satellites into smaller parts, sometimes even functional satellites will collide and fracture, or launch vehicles may eject particles of fuel. A small number of deliberate ground-to-space anti-satellite (ASAT) weapon tests have also exploded defunct satellites, creating outsized amounts of debris compared to accidents.
Image
So the amount of debris in space depends on the number of new objects being launched into space. But the amount of debris is a stock, and new objects are added as a flow. The number of new satellites being added to orbit has increased precipitously, while total debris also appears to be growing, but more smoothly.2 Both new launches and collisions between active satellites add debris, but debris also naturally re-enters the atmosphere, so the total amount of debris doesn't necessarily increase over time.
Debris is more spread out across altitudes, while satellites in low Earth orbit (LEO) tend to be clustered around the 550km altitude bracket.3 Still, most mission-ending risk for a rocket launch is posed by passing through LEO, because at much higher altitudes debris is simply less dense in space. The ESA reports more than 650 fragmentation events to date, but only four confirmed collisions between catalogued objects: most impacts involve untracked small debris, rather than collisions with tracked objects.
More than 95% of mission-ending collisions are caused by "lethal non-trackable" objects in the range of roughly 1mm–1cm diameters. Larger than this, and the object is trackable, and active satellites can manoeuvre to avoid them. Much smaller than this, and the collision is survivable. The distribution of objects is very roughly a power law with size, with around 100 million objects in the 1mm to 1cm range.
Image
When could debris block transit through orbit?
The important question here is whether, for a given amount of debris and satellites in orbit, a spacecraft can successfully pass through Earth's orbit (without a mission-ending debris collision).
We can model low Earth orbit as a shell volume, with homogenous debris in uniform spatial distribution. All fragments of debris are identical in mass, travelling at the same speed relative to the spacecraft (in ). The spacecraft presents a constant cross-sectional area (in ) against the direction of travel of the debris fragments, and travels at uniform speed directly through the orbital volume over duration . represents the volumetric (number) density of objects which the spacecraft could collide with, in count . The spacecraft fails if it collides with any debris fragment.
Then the expected number of mission-ending collisions is just:
The chance of failure is:
We can figure this out with current numbers. First we need to know , the time for a spacecraft to pass through LEO. This depends on the altitude of the LEO volume, and the ascent profile of the spacecraft. Let's say that the volume extends from 250km to 1,250km in altitude, since this is where most debris and satellites are. The most direct way to figure out the spacecraft's ascent profile is to look at empirical data for launches to LEO, which show average velocities of around 1–2km/s. True speeds for beyond orbit are faster but not significantly so the required to escape a planet's gravity is always a factor of larger than the required to enter orbit), so we'll go with 2km/s. This gives 500 seconds ≈ 8 minutes passing through the debris zone, implying a launch distance of about 1,000km, although of course ascent profiles vary. This seems reasonable, since most objects in LEO fit in a 1,000km band; but note that higher (and much sparser) orbits extend to around 35,000km in altitude.
Estimating the current chance of a mission-ending collision during a launch through orbit
One fast but kludgy way to estimate the chance of collision during launch is to consider the 'natural' lifespan of a typical active satellite in a preferential low-Earth orbit. That is, the expected lifespan if it isn't deliberately decommissioned and cannot manoeuvre away from debris. This annual (lethal) collision rate for active objects currently appears to be around to , giving a current expected lifespan of a satellite of somewhere between 1,000 and 10,000 years.4 For the rocket's , I'll use .
On the model above, then, we can substitute for , where subscript indicates an average satellite, and indicates the rocket or spacecraft launching beyond Earth:
Here is a year, and . I'll assume for the average cross-sectional area of these satellites. Substituting for in this way, we get the following:
I estimate to be , since some orbital collisions are head-on, while others are more like low relative velocity grazes. So ultimately we don't need to know directly, but we might want to use it to get an estimate for (the spatial density of debris) of around, so for that purpose I use . Using our estimated range of between and for observed lethal debris flux, we get an estimate of of between 3 × and 3 × .
We can validate this number by looking at direct estimates of spatial density from this report, which suggests the spatial density of objects larger than 1mm in diameter averages between and across preferential orbits in LEO (the range is given by the disagreement between the two models). That the number here is 10 to 10,000 times higher than the estimate derived from the frequency of observed collisions isn't so surprising, because presumably only a fraction of impacts cause a lethal (mission-ending) collision.
We have a choice about what value of to use here: are we considering all debris, or just the debris which in fact is observed to cause lethal collisions on impact? In the first case, comes out to be between 3 × and 3 × . In the second case, the estimate is more like . I suggest the latter option: estimating based on observed collisions, implicitly factoring for the level of protection that satellites already have on average. So I suggest a central lethal debris flux estimate of .
Finally, plugging the numbers into the equation, we get:
This is exceptionally and unsurprisingly low. It suggests one mission-ending collision per 2 million launches to space at present-day levels of debris in LEO.
The reason it is so low is almost entirely because a launch beyond orbit only spends a few minutes passing through the hazardous zone, whereas satellites stay in it for years. Imagine a standard-width highway where all the cars travel extremely fast, in both directions, but there is no convention for which side of the road to drive. Imagine the cars are each spaced out by a few kilometres. You are far less likely to be hit if you run across the road at a random time, compared to taking a road trip of a few days along the same highway.
Accidental Kessler syndrome
Kessler syndrome is "a situation in which the density of objects in low Earth orbit (LEO) becomes so high due to space pollution that collisions between these objects cascade, exponentially increasing the amount of space debris over time".
Although sophisticated models of orbital debris exist, I've found it difficult to find "best guess" analyses of the conditions which would make Kessler syndrome likely, or estimates of how severe the result of Kessler syndrome would be. So in the "workings" section below, I run through some of the numbers and suggest some basic (and very tentative) models to help understand Kessler syndrome in simple terms.
One takeaway for me is that, on reasonable parameter estimates, accelerating growth in the amount of space debris does actually seem more likely than not, given both a large uptick in the amount of debris being launched into orbit, no significant increase in rates of disposal or cleanup, and non-compliance with disposal rules. Because of the faster-than-exponential nature of growth, it's not crazy to imagine that humanity would reach a point in the next few decades where we're not able to curb a runaway scenario until it levels off; though cleanup operations could continue to help. As mentioned, this is based on a simple "source-sink" statistical model of the Kessler dynamic. More detailed analysis since Kessler (1978), including more granular modelling of fragmentation dynamics, suggests that the carrying capacities of at least many orbits are larger than naively imagined.5
How much more debris after accidental Kessler?
I found it difficult to estimate just how much more 'crowded' Earth orbit (especially LEO) would become in the aftermath of Kessler. My first estimate considers how many collisions with "small impactors" currently occur in orbit (surprisingly few), how many more fragments of debris would be created with the mass of all the new satellites added before Kessler syndrome begins, and how that would effectively increase in the launch risk model above. Without correcting for simplifying assumptions, I found increases by a factor of 100 to 1,000.
One crucial simplification is how much debris fragments from satellites further break down from debris-debris collisions. I'm not exactly sure how to measure this, but assuming a specific power law estimate for the actual size distribution of space debris, and then assuming all of that debris is "ground down" into what I consider to be a worst-case size range of 1mm–1cm fragments, I find that the density of debris becomes 400 times worse, making space at least 400×100=40,000 to 400×1,000=400,000 times more dangerous for launches beyond orbit than the present day. This gives us a best-case to (extremely) worst-case range of around 100 times worse than the present day, to around 100,000 times worse.
I may also be underestimating the sheer mass of objects being launched into space in the future, since I didn't model exponential growth in launch mass, but rather a sustained number similar to the present day. So let's add a further (somewhat extreme) factor of 50 to account for this potential underestimate, making space 5,000 to 5 million times more dangerous than today. Let's take a worst case-leaning number from that range: 500,000 times worse.
In this case:
In this post-Kessler case, then, each launch is expected to incur 0.25 collisions on average. The chance of success is . This implies at least higher cost per successful launch6 (because of the need to launch about 1.28 spacecraft for one to make it through in expectation). This is a noticeable difference, but certainly not sealing off the possibility of leaving Earth.
As I'll discuss later, it could be that costs increase by less than the proportional increase in , because of mitigating measures like shielding (or surface-area minimising trade-offs). The cost of operating satellites would similarly increase to the new cost after installing more aggressive collision-avoidance and tracking systems, thicker shielding, and more expensive direct-injection launch profiles that spend less time in congested shells.

Image
That said, as I'll explore below, there is a point not far from this estimate of (in terms of the spatial density of debris) where launches become entirely impossible without better protections such as shielding. Further, even for smaller amounts of debris, failed launches could themselves contribute to the amount of debris in orbit, and this dynamic could much extend or worsen the post-Kessler period where launches are inaccessible.
So, I tentatively conclude that ‘natural’ kinds of Kessler syndrome are unlikely to make space inaccessible. This is for a few reasons: in part, because I was using fairly worst-case assumptions. In part, because accidental Kessler syndrome eventually recovers with time as smaller particles of debris fall to Earth by atmospheric drag. But mainly, because I haven't yet considered countermeasures to debris, especially debris cleanup. Although I don't consider countermeasures in depth, I hold out some hope in line with the pace of innovation and cost declines in (for example) green energy, which surprised many. For example, early prototypes and suggested designs include nets and lightweight foams.
That's not to weigh in on the cost of being no longer able to operate satellites in LEO, which would be considerable, and could have security implications because of the extensive use of satellites for reconnaissance and verification. That said, I don't think losing access to LEO for satellites would be catastrophic on economic grounds. Suggestively, the private space industry is currently valued on the order of $1tn, similar to the market capitalisation of Netflix or Visa (though of course Netflix is not critical infrastructure). The main losses would be weather monitoring, infrared nuclear missile detection, and Earth observation and sensing, which is often used for verifying arms control agreements. It's these last two uses which strike me as likely most important, and I expect losing these capabilities would be geopolitically destabilising, because they could make a first strike more appealing. 7
Deliberate debris dispersal
Deliberate forms of adding debris to orbit involve launching mass into orbit with the intention of making orbits inaccessible or prohibitively expensive, for satellites and potentially even launching beyond Earth to outer space.
This is different from using an ASAT weapon to convert the mass of existing and intact satellites into debris, because it's not constrained by the mass of debris already in orbit; or the size distribution of that debris after fragmentation events. I also don't think we have to assume this would count as deliberate Kessler syndrome. Kessler syndrome involves a runaway feedback loop, where debris-debris collisions increase the amount of debris. But it could be that the debris is already broken up when it is launched, in which case the Kessler dynamic wouldn't be an important aspect of deliberately adding debris into orbit. In other words, if Kessler syndrome turns out to be hard or slow to trigger, we shouldn't stop worrying about deliberate but non-runaway modes of adding debris to orbit.
Moreover, Kessler syndrome is eventually self-limiting. As discussed elsewhere, particles of debris fall to Earth by atmospheric drag.8 And as fragments of debris break into smaller pieces (from the size of tennis balls, to grains of sand, to motes of dust, to smoke-sized particles), their expected remaining lifespan in orbit falls from years to months to days. So if some actor wanted to deliberately sustain a large amount of debris in orbit, they would have to constantly replenish it.9
Effects on launch cost
In the "workings" section below, I consider the expected number of collisions for a given mass , assuming the mass is broken into optimally sized particles travelling at orbital velocity in LEO, around 1mm in diameter.
Here's the general version:
Where is the diameter of the particles of debris, is the density of the debris, is the Earth's radius, and and are the upper and lower altitudes of the orbital volume. Note that, if the goal of debris dispersal is to block specific launches, it very likely cannot target specific regions. Although equatorial launches are preferred, there is no "Gibraltar-style" chokepoint for access to space, and debris naturally disperses across orbits.
Plugging in some conservative estimates, we get:
Note that I make two worst-case assumptions here. First, that all pieces of debris would cause a mission-ending failure on collision. Remember that this is very likely not currently the case for satellites: I estimate at least 99% of potentially lethal collisions are currently avoided either by manoeuvres or shielding. Second, I assume that all debris is broken down into the optimal size. In other words, it would take about 25× less debris than the case I consider where debris is naturally "ground down" in the aftermath of accidental Kessler syndrome to a "worst case" size distribution of 1mm to 1cm. And recall further that I estimate this "grinding down" process would make the number density of debris fragments about 400 times worse than the current size distribution of debris fragments. I validate this against my previous method of estimating launch failures in the workings below.
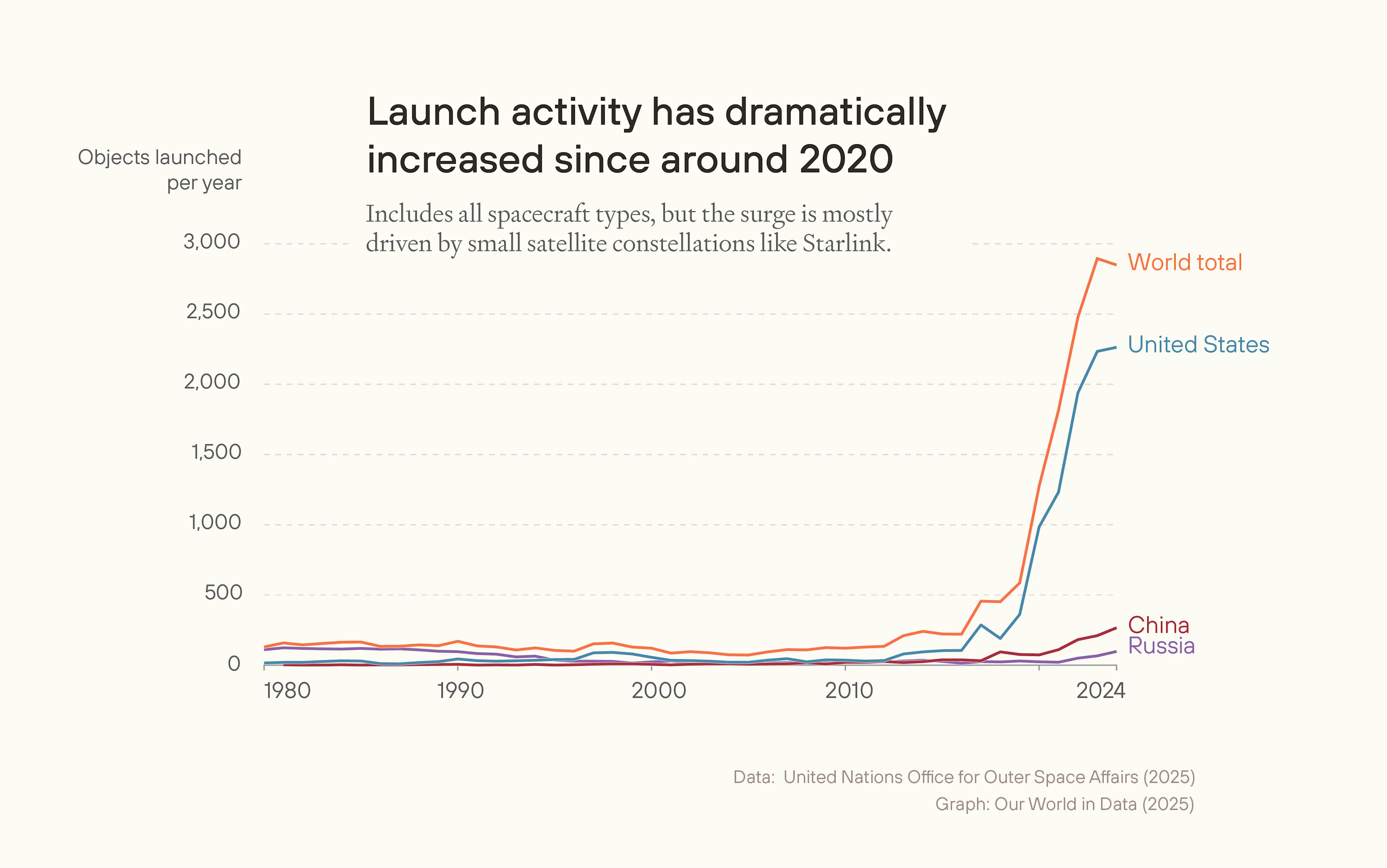
For example, to raise to 100, we see we need about kg, or 58,000 tons (call it 60,000). About 2,000 tons were launched into orbit in 2024 as payload, and launches are increasing by very roughly 30% per year, with the cost to launch a kg of payload also decreasing.
As noted above, the probability of success per launch is . With launches the probability of at least one success is then . A very important feature to note is that the number of launches needed to make at least one success likely grows much faster than the expected failures per launch (exponentially faster). When is large, the number of launches to make success likely is . So if , we would require far more launches than there are grains of sand on Earth, to expect at least one to succeed. On this model, launch would indeed be entirely prohibited. Any possible countermeasures or defences against debris will have to be effective enough to bring the risk per (potential) collision into the rough ballpark of the chance of a commercial flight surviving a bird flying into the engine (about per bird). In fact, launching beyond orbit would already become vastly expensive with , where , requiring only around 6,000 tons on our worst-case assumptions.
At what point will effectively blocking launches become available to a single actor (such as a single country)? One source estimates the experience curve for SpaceX launches, that is the percentage decline in cost to launch a given mass of payload per doubling in cumulative launches, finding a fit to the data of 61% decline in cost per cumulative doubling. The number of commercial launches has been increasing around 30% per year, so the growth in cumulative launches will itself approach 30% per year (from below). This is about 0.38 doublings per year, so a cost decline of around 23% per year. In 2019, Falcon Heavy was lifting 1kg to orbit for $1500; let's call it $1000 today. So the cost to launch 60,000 tons of pure debris at roughly present prices is around $60bn, or 6,000 tons at $6bn; this is already surprisingly affordable. After 15 years of cost decline, we can expect prices to fall to roughly 2% of current levels, that is $1.8 billion total for 60,000 tons, or $180 million for 6,000 tons.
Image
In fact, already Starship's payload capacity is around 150t, so at the lower end of our estimated debris needed to block launches, we're talking about roughly 40 Starship launches being sufficient. In this case, the blocker to launching enough debris from Earth to cause massive difficulties and disable virtually every satellite in LEO does not seem to be monetary cost. I expect there will be major blockers, but I expect them to mostly come from political barriers and mitigation technologies (more on that below).
In other words, without some radically new method for mitigating collision risk from debris, an actor inclined to haul enough debris into orbit to make launches into outer space near-impossible probably could do so for less than $1bn before 2040. This makes the prospect of deliberate debris dispersal tentatively concerning, in the sense that we would need to rely on detection and prevention methods to stop bad actors from causing it, and/or launch methods which mitigate the risk.
Again, however, note these estimates are made with fairly worst-case assumptions about the size distribution of debris, and the mission-ending risk per debris fragment. In practice, I expect the actual amount of debris required to be much (perhaps 10 to 1,000 times) larger to reduce by the same amount even without mitigations.
Summary table
Here's a visual summary of some of the numbers so far. is the expected number of collisions per year for a typical satellite in LEO; and is the expected number of collisions, per launch, for a rocket passing through LEO into outer space. The numbers for are given by assuming the collision risk scales equally with rockets. Obviously the numbers remain very approximate, so I give very approximate numbers. For , I've taken the geometric mean of the initial range.
| Current debris | to | |
| Natural Kessler aftermath (pessimistic) | 2 | 0.005 |
| Natural Kessler aftermath (pessimistic, 50x total mass) | 100 | 0.25 |
| 6,000 ton deliberate debris dispersal (pessimistic) | 5,000 | 10 |
| 60,000 ton deliberate debris dispersal (pessimistic) | 50,000 | 100 |
Motivations for deliberate debris
It's hard to think of any prosocial reasons for injecting thousands of tons of debris into orbit. Still, we might imagine that it becomes impossible to verify the payloads which are being launched into outer space, and so (through some democratic or accountable process) the world agrees to make it practically impossible to send probes beyond orbit, before some suitable period for humanity to remain Earthbound, and agrees that the best way to do this is to crowd Earth's orbit with debris. This seems possible but very implausible to me.
Another possibility is that a world power chooses to inject large amounts of orbital debris to neutralise an adversary's access to ICBM launch capability. ICBMs spend most of their flight path at LEO altitudes (160–2000km) before re-entering the atmosphere. A major power afraid of long-range nuclear attack by ICBM could essentially defend themselves against the possibility, at the cost of removing their own launch ability.
I don't find this especially plausible, either, for a couple reasons. First, other delivery mechanisms exist which stay in the atmosphere, like scramjet hypersonic missiles or 'hypersonic glide vehicles'. Second, deliberately injecting thousands of tons of debris would cause so much collateral damage — knocking out (likely) a more than trillion-dollar private satellite industry, and rendering their own surveillance satellites obsolete. The reaction from the international community would surely make such a move a total non-starter for any power engaged in trade. But it could remain a concern for an isolated rogue state like DPRK.
Exclusive access
A potentially more concerning motivation for deliberate debris injection is that some actor could use it to lock-in exclusive access to outer space. This could happen in a couple ways.
First, some actor whose major presence remains on Earth could first send 'totipotent' craft beyond Earth, such as to the Moon, other sites in the solar system, or other stars. Second, their remaining presence on Earth could inject massive amounts of debris into orbit, essentially sealing off the ability to access outer space for long enough that the presence beyond Earth can achieve strategic dominance over outer space.
By 'totipotent', per Toby Ord, I mean "any system which is fully independent, self-sustaining, and able to eventually achieve anything that humanity-on-Earth could eventually achieve", where the third point implies the first two. Most likely, I guess this involves uncrewed (robotic) spacecraft, with far more advanced technology than today's, capable of collecting resources and useful energy in order to spin up mechanised industry — perhaps in order to make and launch more spacecraft of the same kind.
By "strategic dominance", I mean a state of affairs where this actor can prevent every other actor from meaningfully accessing outer space, indefinitely, including through the use of threats (or eventually through defeating or converting other actors).
A few things to say about this possibility. If an actor on Earth begins to inject massive amounts of debris, they will surely meet with serious resistance from other actors. This resistance could easily be enough to prevent them from succeeding, especially since launch sites are very hard to conceal and easy to sabotage (e.g. through targeted munitions).10 Other actors could even try to catch the window where outer space remains accessible, and launch their own craft to catch up. These craft do not need to be totipotent to prevent the first-moving actor from seizing outer space; they just need to be capable of stopping or delaying them enough. Even if the bad actor succeeds, we can imagine the rest of the world is more likely to form a coalition against the bad actor, to forcibly disempower them. If the rest of the fails, and the bad actor succeeds in establishing a hegemonic on Earth, it's not clear why they had to go to the trouble of sending a totipotent craft first, and then launching heaps of debris into orbit. It seems like the strategy of directly establishing world hegemony (though likely just as bad from a global perspective) would have rationally dominated from their perspective. If the rest of the world succeeds, they may have been delayed compared to how early they could have launched their own totipotent craft, but maybe not — it's a separate question how long of a lead time a first-mover in space needs to establish a robust first-mover advantage.
Second, some actor could first establish a totipotent presence in outer space, such as on the Moon. Then that off-Earth presence could inject massive amounts of debris into orbit. They would do this to the same end, that is sealing off access to outer space from the rest of the world, indefinitely, and so effectively 'seizing' access to space for themselves. A major difference is that it could be more difficult for the rest of the world to forcibly prevent the first-moving actor from successfully acting on this strategy, by the time they begin.
In particular, the first-moving actor could establish some industrial presence on the Moon (for superficially innocuous purposes), and then inject Moon rock into LEO. The energy cost to inject the same mass of Moon rock into LEO is smaller than the cost to launch the same mass from Earth's surface, because of the Moon's smaller gravity well.11 I consider this scenario in the next section, and conclude that it is likely much less practically feasible.
Methods for deliberate debris
We can consider two cases: launching debris from Earth into orbit, and launching debris from the Moon. If launching from Earth, much of our analysis above applies. The most direct method would be to find some ideal substance (such as very fine sand, or mm-scale metal ball bearings or lead pellets), load it into some container, and release it at some point in LEO. Debris created at a point in LEO quickly disperses on the order of weeks to months; but to accelerate this process, the actor could use explosives, perhaps constrained to the lateral direction (parallel to the Earth's surface) to minimise debris lost to atmospheric drag or to oblique orbits.
One issue is that, today, orbital payloads are almost always inspected quite carefully. Normally this is for voluntary reasons: the satellite manufacturer really doesn't want their satellite to fail. But there are also contractual requirements on the part of the launching party, for example SpaceX inspects everything their launches carry, to mitigate against failures during launch. In practice, I would guess that the bad actor either needs to be working with (or to be) a nation state, or large launch company. Even then, I expect it would require a fairly extreme level of cover-up for the rest of the world to ignore that you are effectively just launching heaps of sand into orbit. More likely, I expect a 'shock and awe' strategy: lining up as many launches as possible in a short span of time. But I even expect this to be prohibitively difficult.
The second case, as mentioned, is launching mass from some established totipotent base on the Moon. The main advantage here is that the energy cost to launch a given mass of debris from the surface of the Moon is much lower than from the Earth. The force due to gravity on the Moon is about a sixth as strong as on the Earth's surface, but in practice the actual cost is even lower than that because of both (i) atmospheric drag, and crucially (ii) the rocket equation, which accounts for the fact that fuel effectively requires fuel of its own to be lifted, which requires slightly more fuel, and so on.
Not accounting for the rocket equation or atmospheric drag, the specific energy needed to "escape" the Moon's gravity is roughly 2.8MJ/kg, and in theory the GPE of some mass falling to Earth can be converted into enough velocity to reach an orbit around Earth. On the other hand, the specific energy needed to reach LEO from Earth's surface is around 32MJ/kg. In practice, the real energy required will be much greater, and the ratio will be even more pronounced.
However, we're idealising away the question of how a mass could be "launched" from the Moon's surface, and end up in LEO. If we ignore the possibility of controlled burns or aerobraking, and just think of the Moon and Earth as two point masses in a vacuum, there is no launch trajectory which stabilises in LEO. This is fairly intuitive: if you throw a mass in Earth's direction, it gradually trades GPE for KE as it passes right by Earth — at which point, it has enough KE (by conservation of GPE + KE) to reach as far out as the Moon on the other side, so the mass is stuck in a highly eccentric orbit. Imagine rolling a marble along a frictionless funnel, so it rolls in a circular 'orbit' around the bottom of the funnel. This isn't possible once you let go of the marble.
The key is that the mass launched from the Moon needs some braking force applied, in order to slow to the speed of a circular orbit at LEO. One option is to use the Earth's atmosphere as an aerobrake, by aiming the mass trajectory to just graze the Earth's upper atmosphere to shed velocity. Probably this has to involve many passes, each trimming velocity until the high eccentric orbit 'circularises' into LEO.
I see two problems with this approach. First, it takes a long time. An object launched from the Moon just enough to fall back to Earth enters into an eccentric orbit of roughly 10 days; and it would have to orbit Earth many times (say, 10–20 times) before settling into LEO. That gives a period of 3–6 months or so for the rest of the world to react, including by trying to destroy the provoking actor on the Moon while they remain vulnerable. Second, my understanding is that multiples aerobraking requires fine ongoing control to subtly adjust the craft's orbit. For a material like sand, where each grain is going to experience different levels of atmospheric braking, I'd expect almost all the sand to be lost to a permanently eccentric orbit, or by falling to Earth. So my best guess is that this method wouldn't work.
A second approach could be to launch vehicles with some steerable propulsive force, containing large amounts of debris as payload, from the Moon into orbit. These vehicles could carry enough fuel to enter into orbit in a single pass, with a massive retrograde burn at perigee, without ever entering the atmosphere. Or they could aerobrake as before, but with the ability to adjust orbit until they are settled into LEO; or some mix of retrograde burn and aerobraking. In any case, the result is that these vehicles settle into LEO, and then release their payload, passively or perhaps using explosives to disperse them quickly. But then you are bottlenecked again by the payload capacity of the vehicles, just like when launching mass from Earth. The bottleneck on Earth was never finding enough payload mass, so this strategy just seems much more convoluted, and the only benefit I can think of is that it could be easier to prepare the payload and launch vehicles with less threat of direct intervention.
A final approach could be to create a cloud of debris in the L1 Lagrange point, which is a common waypoint for launches beyond Earth. I doubt this makes any sense for two main reasons. First, without active guidance, the debris would quickly disperse, since L1 is gravitationally unstable. Second, multiple transfer families bypass L1 (or any single waypoint).
Detecting and preventing debris dispersal
One way to make deliberate debris dispersal less likely is by reliably detecting attempts to do it. As mentioned, I think that it would already be very difficult to inject thousands of tons of debris into the atmosphere, because launches are very expensive events which involve many overlapping kinds of inspection by default, even if these inspection methods are not explicitly looking for weapons. That said, it could be possible to explicitly require inspections, and we could imagine international agreements to this effect, enforced in a similar way that nuclear agreements are enforced by the IAEA.
Launches from the Moon might be harder to detect by default, but we could imagine a regime where the actor on the moon agrees to surveillance of their launches and their payloads, perhaps with some override mechanism. This wouldn't need to be sophisticated, since the dangerous payload is, after all, hundreds to thousands of tons of debris.
A final possibility is that, even with large amounts of debris in orbit, actors not responsible for dispersing it could still reach outer space by better methods of shielding, avoidance, or some other mitigation. I am quite hopeful here: currently, the rate of small impactor collisions seems low enough compared to the expected lifespan of most satellites without impactors, so I expect it's currently not worth investing a whole lot in protecting a satellite against them. As such, even the small observed frequency of collisions likely overstates the possibly much lower danger with more advanced protections or mitigations.
One point of reference here is the International Space Station. The ISS is about 100m × 70m at its widest points; although its cross-sectional area presenting against the direction of travel of most pieces of space debris is smaller than a full 100m × 70m area. Solar arrays dominate the CSA, presenting perhaps 1,000–2,000m². The main truss and pressurised modules maybe present something like 200–500m², for around 2,000m² total. The ISS has been (mostly) continuously crewed and operational for some 24 years. Above, I assumed a typical satellite presents around 100m² in cross-sectional area (), so the ISS has accumulated around 10–20 times more collision risk than a typical satellite, or around 200–400 "satellite years" of exposure.
But it hasn't been destroyed, or even gotten close to being destroyed. One reason is that, unlike most satellites, it's possible (or rather, considered economical) to make repairs to the ISS; so small damage needn't be immediately or cumulatively mission-ending. Indeed, many collisions with small pieces of debris are not mission-ending even without shielding: debris can blast a clean hole in a solar panel without compromising the rest of the craft. But that's not true for the valuable and pressurised parts of the craft. So what explains the survivability of the ISS? I think there are three main considerations here.
One minor reason is that the ISS orbits at a lower average altitude (400–420km) than most operational satellites (500–1,200km), and lower than the point where debris is most concentrated (around 550km). This is because there's a tradeoff between launch costs, debris exposure, and radiation exposure on the one hand; and atmospheric drag on the other. Because the ISS is so valuable and large, it can afford to periodically boost to maintain orbit at such low altitude. But this means that the low frequency of damaging collisions with the ISS is going to underrate the hazard that most satellites would be exposed to after a Kessler event, and overate the effectiveness of proactive measures like avoidance and shielding. But I think this is a relatively minor consideration — I roughly guess the difference in exposure to debris is a factor of 10–100.
The second consideration is active collision avoidance from trackable debris objects. NASA's guidelines require the ISS to maneuver if any tracked object comes within a "pizza box"-shaped area roughly 2.5 by 30 by 30 miles (4 by 50 by 50 km) with the ISS at the center. The ISS has performed more than 40 collision-avoiding burns since it was deployed in 1999. Objects must of course be trackable to be deliberately avoided, and anything smaller than ~5-10cm cannot be tracked with current systems. I'm unsure how high the false positive rate is, but I'd guess it's high, i.e. I'd guess most manoeuvres are precautionary but ex-post not necessary.
In the context of launching a rocket through the atmosphere, active manoeuvres might be less promising. Typically the ISS operators are notified of some risky piece of debris days in advance, and manoeuvres are made hours before any possible collision. I imagine the challenge of manoeuvring well clear of a roughly 1,000km cross-sectional area containing a tracked object with hours of notice is vastly easier than manoeuvring clear of debris with at most minutes' notice, and when the trajectory of the rocket can only be changed by a few degrees.
That said, it would be possible to check the projected rocket trajectory against the trajectories of tracked objects. Unless there are virtually no launch windows which avoid a tracked object with confidence, this strategy could dramatically cut the risk from tracked objects. The issue, of course, is that most risk-posing objects (of diameter ~1mm to 5cm) are not tracked or even trackable with current technology.
The third consideration is shielding. It turns out the relevant physics of shielding changes a lot when we're considering small hypervelocity objects (say, ⩾3km/s) compared to more massive but slower objects, including most bullets. At familiar projectile velocities, the most mass-efficient way to stop a projectile is with a "slab" of material, like an aluminium wall. For small debris fragments, the main force acting on the piece of debris on collision is the instantaneous pressure of the shielding material, not its material strength (before it yields). This means that even very thin shielding like aluminium foil exerts a large enough force due to pressure to fragment and/or vaporise into a cloud of much smaller particles. This makes it comparatively easy to spread out the energy of a piece of debris over a large area.
This effect is exploited by "Whipple shields" or some variant (e.g. adding in some kind of compressible material between the layers). The basic idea is that a thin, foil-like "bumper" spreads the energy of incoming debris, which is then much easier to absorb with a wall layer of thicker shielding. The ISS is equipped with shielding like this, which is hit frequently, including on crew module windows. The vast majority of these impacts are too low-energy to pose much risk anyway, but statistically they surely do include fragments in the "lethal non-trackable" range we're worrying about in this research note. These general considerations are also true of other large, highly valuable satellites in orbit, like the Hubble telescope, Tiangong station, and large radar satellites like TerraSAR-X.
The most obvious way to model improvements to shielding is to consider it as a way of reducing the fraction of debris particles of all sizes that succeed in causing a mission-ending collision. Recalling our expression for success above:
Originally we considered that all collisions with particles of debris in the mission-ending range cause failure. Instead, we can take to represent mission-ending collisions, and add a term for protection, standing for the fractional increase in (previously mission-ending) collisions needed to reach the same number of mission-ending collisions as with no protection:
This is a very simple effect. For high , the number of launches needed to expect at least one successful launch grows exponentially with ; whereas the increase in needed to expect at least one successful launch grows linearly, with . So shielding and other kinds of protection scale better than increasing the number of launches.
For engineered Kessler syndrome, we previously estimated a feasible of roughly 100 collisions per launch. So the question is whether improved shielding can reduce the risk more than a hundred-fold, or 1% risk of failure per potentially mission-ending collision. This seems quite doable.
We shouldn't understand in totally stochastic terms, i.e. as a constant reduction in the risk posed by any given piece of debris. Rather we should roughly understand it as a threshold effect, where an increasingly small fraction of all pieces of debris (by size, kinetic energy, or region of the craft they collide with) have any chance of causing failure.
So the question is whether shielding can eliminate mission ending risk from at least 99% of lethal non-trackable debris (the "worst-case" size distribution). A 1cm diameter piece of debris with the density of aluminium has a mass of around 1.4 grams; let's imagine a 2g fragment of debris. Let's say 10km/s relative velocity (orbital velocity at LEO is around 8km/s). That's a KE of 100 kilojoules, equal to the energy released by about 24g of TNT. Finally, we imagine a "standoff" gap between the Whipple bumper and the rear wall of 20cm, which is on the wider end of the shielding on the ISS. This paper suggests after impacting the bumper and shattering or vaporising, the debris would spread over a cone with a half-angle of around 30 degrees, impacting with the rear wall across an area with radius of around 10cm. We can already see why Whipple shielding helps so much here — the pressure exerted on the rear wall is reduced by times.
There is a literature on finding the limits to protection of Whipple shields. The modelling gets complicated, but the key point is that the critical thickness of the rear wall to stop a given piece of debris scales roughly linearly with the KE of that piece of debris, and inversely with the square root of of the standoff distance. We also see that the required wall thickness scales to the 3/2 power with the diameter of the fragment.
Using the assumptions above about the size and speed of the debris, we can use an equation from this literature to estimate the minimum thickness of rear wall needed to stop debris fragments of that size, and we find it needs to be around 0.66cm thick if made of aluminium (workings in the appendix).
We can make even more conservative estimates if we assume we can't use a Whipple shield to scatter the impact of the debris fragment. This could be relevant in the sub-hypervelocity regime, if debris fragments don't fully shatter or vaporise. Using the same assumptions as before, again assuming aluminium shielding, I find that the wall thickness required for aluminium is around 4.6cm.
That is quite a lot of shielding. The first and second stages of the Falcon 9 together weigh around 30 tons without fuel. The entire rocket is around 50m high and 4m across. Treating its surface area as an open cylindrical shell, that gives of shielding by area. At constant thickness of 4.6cm, that's 600×0.046=27.6m³ by volume. At 2,700kg/m³ that's about 75 tons of shielding required to stop roughly worst-case debris fragments. By comparison, if we only needed 0.66cm of shielding per the Whipple shield case, we'd need (0.66/4.6)×75 ≈ 10 tons of extra shielding, assuming negligible weight for the buffer layer.
In both cases, though, note that this is not all additional weight, because the tanks and fairing already have some bulk to them. Rocket tanks (which present the largest CSA and are typically not well-shielded by default) are normally around 0.5cm thick. That suggests that, with Whipple shielding, the rear wall would not require much additional reinforcement and weight at all. On the other hand, if a Whipple shield doesn't work to break up the fragments of debris, then the additional shielding required could be very onerous. That could be the case if the debris material can be optimised for penetrating Whipple shield without shattering or vaporising, which is a materials science question I know little about. On the other hand, adjusting for the rocket equation would adjust the additional shielding needed upwards, since more shielding mass requires more fuel, which requires more volume, more surface area, and in turn more shielding.
That said, the mass required to shield a rocket scales favourably with the size of the rocket, because surface area scales with the square root of volume. So if thick shielding is needed, rockets could just be made very large, carrying a lot of fuel. For example, the existing Starship design has a payload mass of around 100–150 tons.
Overall, then, I come out feeling optimistic that shielding can be used to significantly mitigate the threat from deliberately induced orbital debris. I think it's more likely than not that, ultimately, the question of blocking launch beyond Earth with orbital debris favours the escaping rockets. That's not even considering more technologically advanced potential options for more active defence.
Conclusion
One extreme concern is that much increased levels of space debris could make launches to outer space extremely difficult; and if so, a bad actor could use that effect to entrench their sole access to outer space. But even with fairly pessimistic assumptions, accidental Kessler syndrome is very unlikely to make transit from Earth's surface through orbit impractical. The launch phase’s brief exposure window through LEO keeps baseline risk low, and hardening (shielding, ascent-path selection, direct-injection profiles) scales better than debris growth. Deliberate, finely-tuned dispersal is the more serious threat to launch economics, but fully “sealing the sky” likely requires tens of thousands of tons of optimally sized material and sustained replenishment. Given inspection, attribution, and political blowback, that’s hard to do quickly or covertly; shielding and scheduling further erode its leverage.
A far more widely-discussed, and perhaps more practically serious concern, is the potential for orbital space debris to take out take out important uses for satellites in LEO, especially remote sensing and communications. If one actor can cheaply "seed" large amounts of space debris, through deliberate dispersal or use of ASAT weapons, they could use that threat as a source of political leverage. As LEO becomes more crowded, the potential damage from such a strategy grows, so vigilance becomes more important. More effectively enforced arms control around the use of ASAT weapons would perhaps be the most useful mitigating measure here. That said, despite outrage around the use of ASAT weapons for "testing", the stubborn realities of arms control negotiations are the main blocker here, not awareness of the problem.
For both sets of concerns, a few other mitigating measures look worthwhile. It may be possible to push down the “lethal non-trackable” risk via better radar or optical sensing, similar to the value of NASA's Spaceguard program for better tracking potential asteroid and comet collisions with Earth. Further, more robust inspection regimes for launch vehicle payloads could help a great deal. Currently, payloads are often inspected and reported for insurance reasons, or to comply with norms or regulatory requirements to report new objects in orbit. But if a bad actor wanted to conceal a destructive device in a rocket payload, my guess is that currently it would be too easy. Lastly, it could make sense for space agencies to increasingly subsidise or directly develop active debris removal prototypes.
I did not consider other launch denial strategies which a bad actor could use, such as sabotaging launch sites, intercepting launch vehicles during their boost phase from the ground, or even targeting launch vehicles with weapons launched from orbit. If not prevented, such strategies could prove far more effective, so I don't omit to discuss them because I'm confident they are less important to consider. That said, I'm similarly hopeful that feasible mitigations exist.
In the introduction, I expressed concern that strategies to block access to outer space could enable a single actor, like a small group or even an individual, to illegitimately seize control over resources in outer space. But I don't think blocking access is necessary for that outcome; so I don't think that mitigating such strategies is sufficient for ensuring access to outer space is more distributed. For example, some actor might grow asymmetrically faster than the rest of the world, grabbing energy and resources beyond Earth before others, further accelerating growth by mostly non-coercive means. Or a single actor could achieve a "decisive strategic advantage" on Earth, before any other actor can create a self-sustaining presence off-Earth (and conceal or defend it).
I'm still very uncertain about some key parameters, both because I'm not an expert, and because of real empirical uncertainties. That includes: post-cascade size–altitude distribution (not total mass), the real-world effectiveness of shielding against worst-case materials at hypervelocity, trends in launch costs, and the geopolitical feasibility of inspections, monitoring, and enforcement against obvious attempts at mass dispersal. In general, I'd very much welcome further work on the strategic implications of faster-than-anticipated increases in launch frequency and efficiency, which looks plausible given an intelligence explosion.
For their helpful comments and suggestions, I thank Toby Ord, Jordan Stone, Aaron Rosengren, Matthew Allcock, Thomas Gonzáles Roberts, and Forethought seminar attendees. Errors remain my own.
Workings
In this section, I work through some models of space debris, and show where some of my bottom-line numbers above come from.
Orbital debris and Kessler syndrome
The 'one-bucket' model, without collisions. We consider , the number of objects in LEO at (in years). New objects are launched at a constant rate , and the quantity of debris declines exponentially with time at some rate . So:
Note that could be negative, because of non-collision fragmentation events like explosions, in which cases debris increases without bound on the model. But space objects are also removed: they naturally de-orbit due to atmospheric drag, or they sometimes deliberately de-orbit themselves, and in future there could be deliberate cleanup efforts that scale with the total number of objects in orbit.
We can estimate based on the number of re-entries in recent years. Pardini & Anselmo (2025) find re-entries on the order of 1% per year (based on the last 5 years of data, assuming constant rate of re-entry per object). Almost all re-entries to date are due to deliberate de-orbiting or natural decay due to atmospheric drag; a negligible fraction are due to debris collisions. So we can liberally estimate , where the expected time in orbit is roughly a century (though each satellite might be operational for a shorter period).
With constant , the number of satellites always reaches equilibrium on this model, where . In 2024 (the last good data point), around 3,000 new objects were launched into space. Assuming no growth in the annual number of objects launched into orbit, the 'carrying capacity' of LEO works out at 300,000 objects, or roughly only 15 times as many objects compared to today.
Alternatively, we can imagine grows exponentially, as it roughly has done over the past 5 years (at roughly 50% annual growth). There is no maximum number of objects in space in this case.
These are something like upper bound cases for the number of operational satellites in orbit for a given , since we're effectively ignoring collisions. Next we'll add in collisions.
The 'one-bucket' model, with collisions. The model is the same as above, but we add a term for collisions between objects. Consider that if the number of objects increases by 1%, all else equal, then the number of objects which could undergo a collision increases by 1%. But, for each object, the frequency of collisions also increases by 1%. So the overall frequency of collisions grows quadratically with the number of objects. So we can add a term to stand for the rate of increase in debris. We get:
Unlike the previous model, this sometimes has no equilibria for constant , and blows up without bound instead. In particular, is a key tipping point: this is the point where blowup is guaranteed even if the rate of launches falls to zero. This is roughly what people have in mind by Kessler syndrome — "a situation in which the density of objects in low Earth orbit (LEO) becomes so high due to space pollution that collisions between these objects cascade, exponentially increasing the amount of space debris over time".
Not every set of parameters blows up into Kessler syndrome. For equilibria to exist, we can set the differential equation above to zero, and find that:
If is higher than this threshold, Kessler occurs regardless of the starting number of objects. However, even when , the system also always blows up if the initial number of objects is greater than the larger of the two equilibria. If there are two equilibria, the larger of the two is unstable, so the important one is the lower of the two. In any case, from playing around with realistic numbers, I think it's unlikely that the current amount of space objects and debris exceeds the upper equilibrium for any reasonable parameter values which have equilibria, so we can bracket this point.
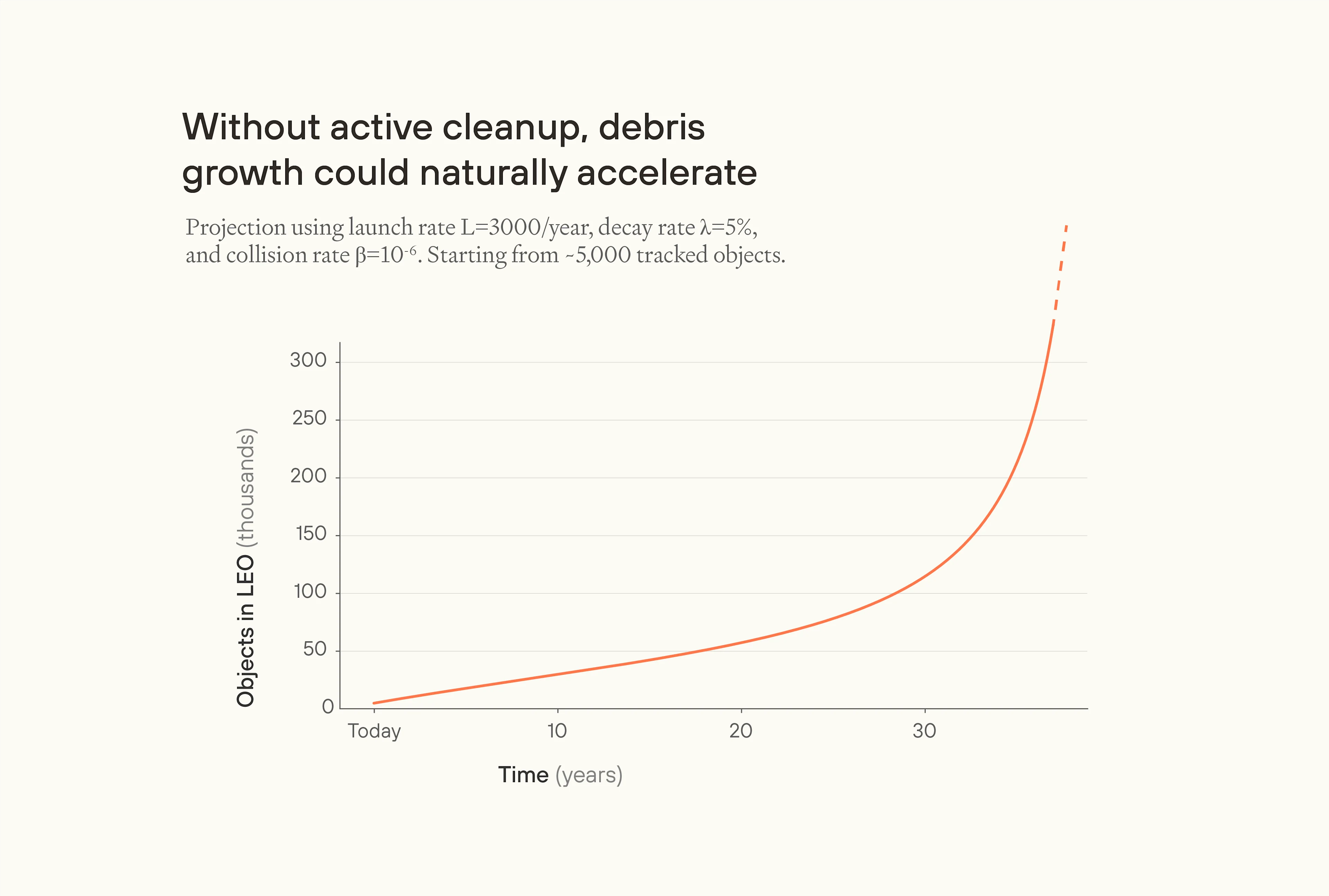
But is Kessler syndrome likely? I found it difficult to find serious attempts to answer the question. Let's consider some reasonable parameter values and see what they show. Nomura et al. is a good source for parameter values. They suggest , based on the observed frequency of collisions of tracked objects, and (i.e. 5% annual net removal) based on the balance of observed non-collision fragmentation events with objects de-orbiting without fragmenting. We set to 20,000.
These parameter values actually do suggest blowup.
Image
In this case: 35 years from now, in 2060, the number of space objects (functional satellites and nonfunctional debris) has grown from around 20,000 to more than 200,000, a 10-fold increase. But the parameter values we chose to be realistic aren't far off from parameter values which do not blow up. For example, take . This reaches a horizontal asymptote around .
We can see which combinations of , , and lead to runaway debris growth visually.
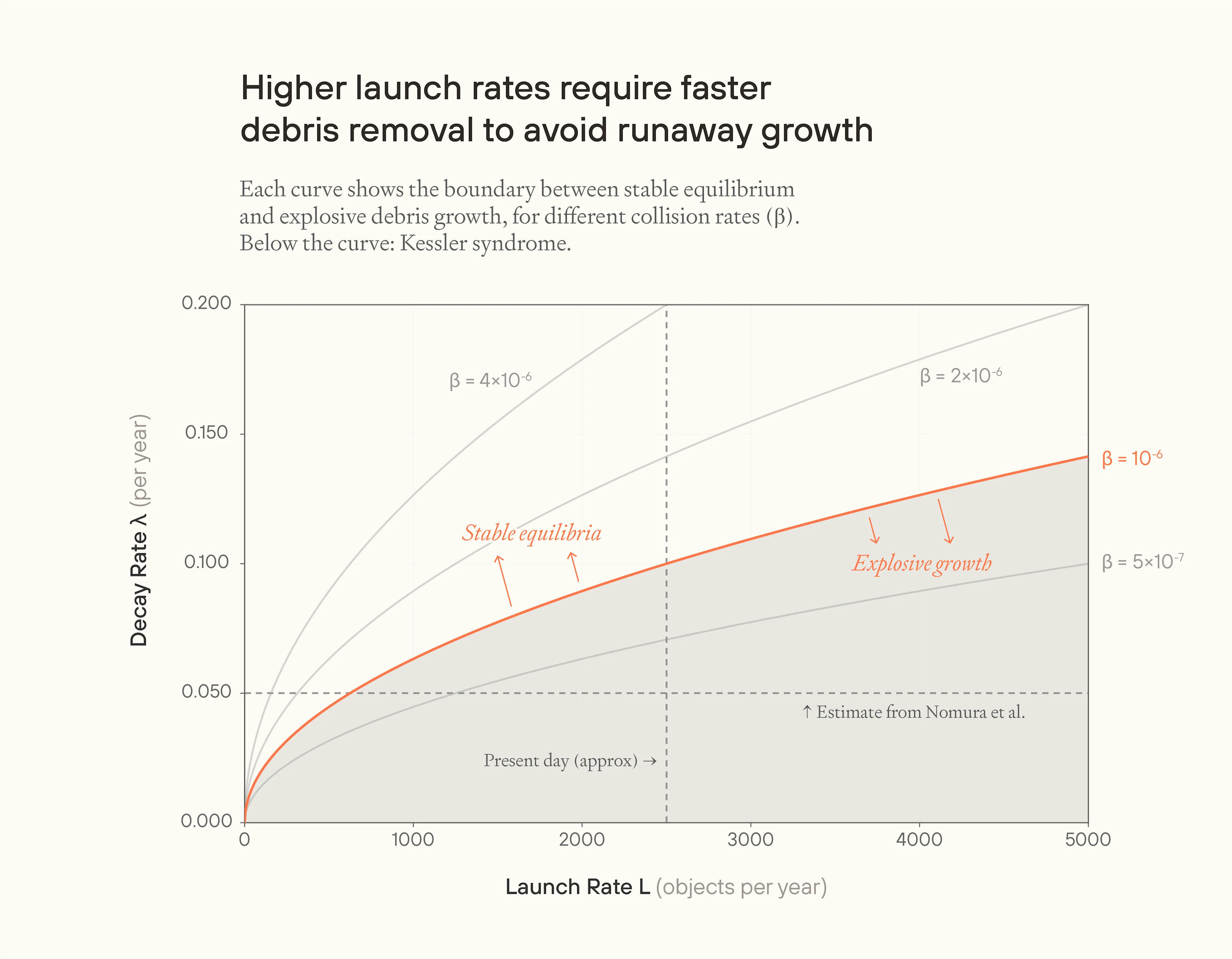
Image
Reflections on Kessler dynamics
One point to notice is that it's somewhat hard to find parameter values on which there is an equilibrium steady state where the number of objects in space is huge without reducing , mainly just because of the empirical estimate of . For space to be so crowded but also settled into a relatively stable 'carrying capacity' scenario, both and have to be very high, and this is a situation where there are vastly many satellites, but each has a very brief functional lifespan (of, say, < 5 years) before being decommissioned. For example, with a lifespan of around 3 years, and a launch rate of 30,000 per year, the equilibrium number of (mostly functional) objects is 150,000, only about 10 times higher than today.
Second, the number of space objects is not the same as the number of functional satellites. In the blowup scenario, notice that most 'objects' are created by a collision, i.e. they are nonfunctional. Consider the case above where we start with 5,000 satellites, launch at a rate of 3,000 (assumed functional) satellites per year, and end up with 300,000 total satellites after 35 years. The total number of new functional satellites launched by this point is 105,000, so if no satellites were rendered nonfunctional, that's 110,000 by the end of the period. But some were decommissioned at a rate of 12% per year, and others were destroyed in the process of being turned into debris! I think this model alone isn't enough to tell us how many satellites are destroyed, because it could be the case that impacts are rare but produce huge numbers of debris objects, or it could be the case that impacts are common but produce a small number of debris objects, and both could give the same value for . But we have to assume that many satellites are being destroyed in this process. Of course as time goes on in a Kessler syndrome, virtually all objects become debris, even with a steady stream of new launches, and the expected lifespan of any newly launched satellite becomes very short.
Third, could be modelled as endogenous, and in particular could be reduced from empirical estimates. Satellites could improve at manoeuvring out the way of debris, debris tracking could improve, and satellite shielding could improve. This stands out as a crucially important factor which is typically overlooked. The result of modelling as endogenous should make us less pessimistic about the likelihood of Kessler, and its speed of onset if it does happen.
Lastly, we should ask: what's going on in the world where the amount of nonfunctional debris is increasing exponentially? I think people will notice, and people can act to change both and , which we've just taken as exogenous. If , then simply preventing all new launches (setting ) would reverse runaway debris buildup. More realistically, could be lowered in advance to some reasonable steady state.
Reducing is capped in how effective it can be compared to increasing (like reducing energy use versus ramping up carbon capture). I don't know much about how promising "active debris removal" methods are, but various methods have been proposed, such as nets for debris, or grabbing satellites and de-orbiting. And if Kessler begins to ramp up, will become increasingly irrelevant, because it doesn't scale with , unlike and .
So, whether the world can coordinate to slow down or halt the rate of launches, I've suggested, is unlikely to be the crucial question. Better decommissioning, avoidance, and especially trash cleanup, could reverse an accelerating trend in the amount of space debris, to a decreasing trend, or a trend which is still increasing but decreasing in the second derivative. The worst-case scenario is one where Kessler is clearly imminent, but the world's reaction is inadequate, perhaps because efforts to improve cleanup (etc.) technology cannot improve fast enough. My rough sense is now that this is more likely than I'd suspected, but still overall unlikely to happen; at a wild guess I'd give it something like 25% by the end of the century, unconditional.
Debris in the aftermath of natural Kessler
Assume that Kessler syndrome does happen, and goes totally runaway before any efforts to curb it can get a foothold. What happens?
On the simple model above, the amount of debris shoots to infinity in finite time. Obviously this won't happen, and the limiting reason is that new material (by mass) isn't being added faster than , rather existing material splits into many fragments.
Suppose, initially, all the objects in LEO are spheres 0.01m³ in volume. After the first few satellites fragment or collide into smaller pieces, each (say) the size of peas, the frequency of collisions does scale roughly quadratically with the number of 'objects' in orbit: since there are far fewer pea-sized objects than functional satellites, most collisions are either debris-satellite or satellite-satellite, and satellites aren't much less likely to collide with vanishingly small pieces of debris than with other satellites.12 But as most objects become debris, then the average size of each object decreases, so effectively decreases just as a product of the changing geometry of space debris. Thus the model will overstate how quickly Kessler blows up, and does not predict some limiting behaviour.
Picture the case where every single satellite of radius splits into 1,000 debris spheres of . A debris-debris collision between two given pieces of debris is the chance that two pieces of debris collide within a CSA 100 times smaller; but because there are 1,000 times more spheres, there are (as before) 1,000,000 times as many opportunities for collision. In general, then, assuming object size is homogenous, as the number of objects scales by a factor of , the average volume of each object falls by a factor of , and so the average CSA falls by . Then the frequency of interactions grows not by but by .
So assuming homogenous size, a more accurate model would be:
Because is smaller on this more accurate model, Kessler is less likely. In reality, we should expect to decrease from something closer to 2 to something closer to 4/3 as Kessler gets underway. So that's one way in which Kessler would self-limit.
A more fundamental point is that, as objects in orbit get smaller and less massive, fewer collisions would result in fragmentation, because the kinetic energy involved () shrinks with the square of relative velocities, but the energy required to fragment some object is relatively constant.
The question here is: suppose you add enough new satellites to orbit until you reach runaway Kessler syndrome, and then you wait. What happens? By hypothesis, the amount (number of fragments) of debris is going to begin increasing, as larger pieces get broken down. As the rate of collisions eventually tapers off, we'd end up with something closer to a homogenous mix (or smooth distribution) of fragments. Eventually, the debris removal processes would begin to dominate again, as fragments of debris fall to Earth.
Questions here are: (i) just how much worse would it be if all the massive objects like satellites were effectively turned to dust; (ii) how long would this take; and (iii) how long would it take for things to return to normal? You could build a model for all of this, but let's just try making direct guesses.
How much more debris after Kessler syndrome? Of around 23,000 objects launched into space in total, around 650 were part of "break-ups, explosions, collisions, or anomalous events". In the last 10 years, around 10 fragmentation events have occurred per year. ESA estimates around 2.5% of these fragmentation events were due to "small impactors" (rather than some non-collision failure). So we can estimate 16 collisions due to small impactors since the beginning of the space age (surprisingly few, to my mind). But this number (the fraction of fragmentation events due to small impactors) has risen to 7.6% in the last 10 years.
Not all small fragments of debris in orbit come from fragmentation events; some are natural meteoroids. But my understanding is that the large majority of space debris (and collisions due to it) come from artificial debris. So we'll assume all debris to date is artificial. We'll also assume that the debris produced by fragmentation instantly fits the long-run size distribution resulting from debris-debris collisions (though we'll revisit this). Using this, we can estimate the tonnage of space debris in orbit, and how it corresponds to the frequency of collisions. Then we can estimate the resulting tonnage of debris after Kessler syndrome.
ESA lists 15,000 satellites still in orbit, and estimates the total mass of all space objects in Earth orbit at just under 15,000 tons. The vast majority of this mass is made of rocket bodies or their satellite payloads, not fragmentation debris. So we can conveniently estimate an historical average of 1 ton per satellite. Assuming that satellites which historically underwent fragmentation events are representative of the overall mass distribution, that gives an estimate of 650 tons of debris.
Frustratingly, ESA simply lists the mass of fragmentation debris at 0 tons. Their report claims "[o]bjects of unknown mass do not contribute to the figures presented", so maybe they are just unwilling to make any estimate, so they claim zero instead. This is fairly confusing, because if you know the mass of a satellite which undergoes fragmentation, then you know the mass of the resulting debris.
In any case, our very rough estimates suggest 650 tons of space debris are responsible for something like 7.5% of all fragmentation events, which currently occur roughly 10 times per year, among a population of roughly 15,000 satellites. Per 10,000 satellites, then, the current mass of space debris is responsible for something like a 0.075/1.5=0.05 collisions per year. How should we extrapolate the per-satellite collision risk as the tonnage of debris increases? In this case, I think not quadratically but roughly linearly, because we're dividing by the number of satellites, and not counting debris-debris collisions. So we can come up with a super simple model of collision risk as a function of the tonnage of space debris, where the annual debris collisions per 10,000 satellites = , where is the mass in tons of all he fragmentation debris, and we estimate to be 0.05.
Then we just need to know the total mass of all satellites when a Kessler event begins. As a ballpark estimate, we can see in our model of Kessler syndrome above that it begins after around 30 years of launching 3,000 new objects per year into space. However, we also need to note that most satellites today are meaningfully smaller and lighter than decades ago, which partly explains the big uptick in the number of objects launched into space. So let's estimate the average weight at 0.5 tonnes, giving 0.5×3,000×30=45,000 tons of debris.
The point of this exercise is to see how bad Kessler could possibly get, even after it becomes practically unstoppable: the total mass of all the debris in orbit does not increase after launches stop. Using our naive estimate, then, we see the annual collisions per 10,000 satellites would be 0.05×45,000=2,250, implying an annual chance of collision of around 22%, and a surprisingly survivable lifespan of around 5 years.
We can now derive an estimate of in the launch success equation. Recall:
Our previous estimate for was to , now it's around 22%. So the new estimate for increases by a factor of around 100 to 1,000.
This is an underestimate, because we assumed that "the debris produced by fragmentation instantly fits the long-run size distribution resulting from debris-debris collisions". In reality, debris would fragment into much smaller pieces than our estimate suggests, because of debris-debris collisions.
I'm unsure how to figure out just how much more debris we'd get from already-fragmented debris "grinding down" even further. But one reasonable method would be to look at the average number of fragments of debris by mass for a typical fragmentation event, and figure out how much larger that number would become as fragments broke up even further, until they settled into some equilibrium.
Fundamentally, this is a question about how the area-mass ratio of fragmentation debris evolves over time.13 I originally thought this "grinding down" process through secondary collisions would increase the A-M ratio by a huge amount (say 10–1,000x), but one key factor is that the smallest fragments are lost most quickly to atmospheric drag; e.g. 1–5mm fragments (which present the greatest mission-ending risk) are lost from 500km altitudes in days to months. So it may be better to think of the initial A-M distribution being relatively fixed, but replenishing over time as larger fragments break into smaller fragments, and smaller fragments are lost.
This strikes me as a fairly important question, but I don't think it's a good use of time to try to model it in detail. One thing I'll note is that models from NASA, especially the 'MASTER' space environment model, assume an unchanging, scale-free size distribution of space debris:
Where is the number of fragments larger than diameter d. What I'm unclear on is how much this distribution is likely to change during Kessler. But we can work out by how much the A-M ratio would increase if the distribution became worst-case, which is where every object falls in the range of 1mm to 1cm (the diameters which pose the largest mission-ending risk).
This depends on the lower bound of the size distribution. In reality, fragments could break up to be too small to be mission-ending, and with a very small lower bound, almost all the mass of debris would become too small to matter. So let's consider a (worst-) case where the lower bound of the distribution is 1mm. In this case, the fraction of total mass lives in the 1mm–1cm bucket according to the distribution above would be about 0.24%.
So, if all the mass eventually settled into the worst-case size bucket, that would be a increase in in the launch risk equation above.
Directly estimating volumetric density of debris
In my working so far, I've estimated increases in collision risk by estimating proportionally how much more debris would exist after some change (such as Kessler syndrome), and then how that would, again proportionally, change rates of collision. I think this is typically a more reliable method for estimating collision, because it routes around uncertainties about mass-surface area ratios.
But we can also directly estimate collision risk by estimating the number density of particles of mission-ending debris. I expect this is a more suitable method for considering the effects of deliberate Kessler syndrome, where the mass-surface area ratios can be deliberately changed. We can also validate or even calibrate this estimate against the known small impactor collision frequency of satellites and rocket bodies in orbit.
Recall the launch failure equation from above:
Here, is essentially the volume swept by the spacecraft being considered relative to the debris, with length and CSA . is a measure of number density (of pieces of debris).
Now, both the volume of the swept area, and the entire volume of Earth's orbit where debris lies, both depend on the 'height' of the orbital volume. Eventually, we'll find that this can cancel neatly. But we'll ignore that for now.
Above, we estimated the effective volume swept by the rocket (relative to debris) at 1km. We can treat the entire orbital volume as a "shell" volume whose inner surface is some lower altitude () above Earth's surface, and whose outer surface is some upper () altitude above Earth's surface. In this case, we can say 500m and 1,500km. The volume is the difference of the two spheres:
Earth's radius is about 6,380km, which is fairly small compared to the difference between and . So we can approximate the volume in terms of spherical surface area times thickness:
Where is the average radius of the shells, which is Earth's radius + 1,000km. This is .
Now we need a way to convert from a given mass of debris, to a number of fragments. In the working above, we saw an empirically estimated size distribution of pieces of fragmentary debris:
With an upper bound of roughly 1m diameter. We also saw that a much more worst-case distribution, where all mass fitted into the same distribution, with lower bound 1mm and upper bound 1cm, involved around 400 times more pieces of debris. Call this the "natural worst-case" distribution. We can add to this an absolute worst-case distribution of pieces of debris uniformly 1mm in diameter.
The absolute worst-case (uniform) distribution of matter would involve roughly 25 times more pieces than the natural worst-case distribution.14 Let's start with that case. For some mass in kg, and debris fragments of density in and volume per debris fragment :
Let's assume , roughly the density of sand. Then , and the mass per fragment , which is indeed about the mass of a grain of fine sand.
Now we have an expression for the volumetric debris density from the launch failure equation above:
Now we can validate it by plugging in our previous estimate of 45,000 tons of debris after natural Kessler syndrome:
This is for the "absolute worst-case" outcome. The "natural worst-case" outcome is 25 times smaller in terms of volumetric density, which gives .
Recall estimates of which today fell between and , and furthermore that I (implicitly) estimated that the aftermath of natural Kessler syndrome would increase by a factor of 40,000 to 400,000 — that is, to , which roughly agrees with the range derived from this approach.
Remember that (implicitly) our estimate of from observed collisions is the number density of particles of debris which in fact cause a mission-ending event on collision, rather than zero or minor damage. The latter interpretation of is the intended interpretation, so we need to adjust our estimate here by the fraction of debris particles which are mission-ending on collision. Above, we found that fraction is in fact somewhere between one in 100 and one in 10,000. Since we're considering a context where the size (and material) of debris is optimised to be destructive (deliberate debris dispersal), it's possible that a higher fraction of debris fragments causes major damage than currently. So — to be conservative — I ignore this adjustment for now, but note that it could make deliberate debris dispersal look 100 to 10,000 times harder than I've suggested.
To summarise:
Now, is the distance travelled through the orbital shell, which we take to be 1000km. We previously guessed . So:
So we can use this method to estimate deliberate Kessler syndrome, which I do above.
Shielding
Here is an equation suggested by this review article for calculating the required rear wall thickness to stop a given piece of debris:
Where:
- = rear wall thickness (cm)
- = projectile diameter (cm)
- = projectile density (g/cm³)
- = bumper density (g/cm³)
- = projectile mass (g)
- = normal component of velocity (km/s)
- = standoff distance between bumper and rear wall (cm)
- = rear wall yield strength (ksi)
We can plug in some of our assumptions here: =1, =2.7g/cm³, =2g, =10km/s, , and =40ksi (from here and here). That gives:
Holding everything else fixed, we can also see that the required wall thickness scales superlinearly with the diameter of the fragment:
We can make even more conservative estimates if we assume we can't use a Whipple shield to scatter the impact of the debris fragment. This could be relevant in the sub-hypervelocity regime, if debris fragments don't fully shatter or vaporise.
Where:
- = wall thickness to prevent perforation (cm)
- = projectile diameter (cm)
- = projectile density (g/cm³)
- = impact angle measured from normal (degrees)
- = impact velocity (km/s)
- And the 0.6 coefficient is calibrated for aluminium targets.
Using the same assumptions as before, with the worst-case , we find that the wall thickness required is:
Bibliography
Badhwar, Gautam D., and Phillip D. Anz-Meador. ‘Determination of the Area and Mass Distribution of Orbital Debris Fragments’. Earth, Moon, and Planets 45, no. 1 (1989): 29–51. https://doi.org/10.1007/BF00054659.
Buchs, Romain, and Marie-Valentine Florin. Collision Risk from Space Debris: Current Status, Challenges and Response Strategies. Lausanne, International Risk Governance Center (IRGC), 2 June 2021. https://doi.org/10.5075/EPFL-IRGC-285976.
Byers, Michael, and Aaron Boley. Who Owns Outer Space? International Law, Astrophysics, and the Sustainable Development of Space. Cambridge Studies in International and Comparative Law 176. Cambridge university press, 2023.
Kessler, Donald J, and Phillip D Anz-Meador. Critical Number of Spacecraft in Low Earth Orbit: Using Satellite Fragmentation Data to Evaluate the Stability of the Orbital Debris Environment. n.d.
Kessler, Donald J., and Burton G. Cour‐Palais. ‘Collision Frequency of Artificial Satellites: The Creation of a Debris Belt’. Journal of Geophysical Research: Space Physics 83, no. A6 (1978): 2637–46. https://doi.org/10.1029/JA083iA06p02637.
Kessler, Donald J, and Nicholas L Johnson. The Kessler Syndrome: Implications to Future Space Operations. n.d.
Kessler, DonaldJ. Collisional Cascading: The Limits of Population Growth in Low Earth Orbit. n.d.
Lewis, Hugh G., and Georgia Skelton. ‘Safety Considerations for Large Constellations of Satellites’. Journal of Space Safety Engineering 11, no. 3 (2024): 439–45. https://doi.org/10.1016/j.jsse.2024.08.001.
Nomura, Keiko, Simon Rella, Haily Merritt, et al. ‘Tipping Points of Space Debris in Low Earth Orbit’. International Journal of the Commons 18, no. 1 (2024). https://doi.org/10.5334/ijc.1275.
Pardini, Carmen, and Luciano Anselmo. ‘Orbital Re-Entries of Human-Made Space Objects: Drawbacks for the Upper Atmosphere and the Safety of People’. Journal of Space Safety Engineering 12, no. 2 (2025): 274–83. https://doi.org/10.1016/j.jsse.2025.04.009.
Ryan, S, and Wp Schonberg. ‘A Review of Whipple Shield Ballistic Limit Equations’. International Journal of Impact Engineering 187 (May 2024): 104899. https://doi.org/10.1016/j.ijimpeng.2024.104899.
Sturza, Mark A, Mark D Dankberg, and William N Blount. LEO Capacity Modeling for Sustainable Design. 2022.
Sturza, Mark A, and John P Janka. REALIZED COLLISION RISK. 2024.
United Nations Office for Outer Space Affairs. Guidelines for the Long-Term Sustainability of Outer Space Activities of the Committee on the Peaceful Uses of Outer Space. United Nations, 2022.
Wen, Ken, Xiao-wei Chen, and Yong-gang Lu. ‘Research and Development on Hypervelocity Impact Protection Using Whipple Shield: An Overview’. Defence Technology 17, no. 6 (2021): 1864–86. https://doi.org/10.1016/j.dt.2020.11.005.








